Chapitre 1 : Outils mathématiques et physiques généraux

Il s’agit dans ce chapitre d’aborder quelques outils de base qui sont considérés comme des blocs élémentaires du calcul en physique. Un étudiant se doit donc à l’issue de ce chapitre de maîtriser les concepts suivants :

• Analyse dimensionnelle d’une équation donnée
• Dérivation d’ordre quelconque d’une fonction de la variable réelle
• Dérivation d’une fonction de plusieurs variables
• Calcul d’incertitude statistique / propagée

1. Analyse dimensionnelle et unités

A. Qu’est-ce qu’une grandeur physique ?

À partir de la définition précédente, on peut donc comprendre que la physique nécessite la mesure de certains paramètres, afin d’étudier, comme indiqué, leurs variations et leur évolution. Une grandeur physique peut alors être définie comme une propriété mesurable. L’action de mesurer permet de comparer par rapport à une référence, afin de mieux appréhender, et éventuellement comprendre.

Remarque : Une grandeur peut être scalaire lorsqu’elle s’exprime par un simple nombre, ou vectorielle lorsqu’elle est exprimée par une direction, un sens, et un nombre.

Exemple : Quelles sont les grandeurs physiques mesurables autour de nous à l’instant présent ?

Il est important de distinguer la dimension et l’unité d’un grandeur physique. Par exemple, “$300 km$” a la dimension d’une longueur, et son unité est le $km$. Une même dimension peut être exprimée dans différentes unités (par exemple, on peut exprimer une vitesse en $km/h$, en $m/s$, en $mph$, en $kn$ …)

Toute grandeur physique peut s’exprimer en fonction de sept dimensions fondamentales, qui forment par ailleurs le Système International des unités.

B. Unités du système international

Le système international des unités se compose d’un ensemble d’unités fondamentales, d’unités dérivées, et de préfixes multiplicateurs.

• La seconde (s), unité fondamentale de temps, est définie comme la durée de 9 192 631 770 périodes de la radiation correspondant à la transition entre les deux niveaux hyperfins de l’état fondamental de l’atome de césium 133 à la température du zéro absolu. (Le césium c’est rigolo : https://youtu.be/uixxJtJPVXk?t=136)
• Le mètre (m), unité fondamentale de distance, définie comme la longueur du trajet parcouru dans le vide par la lumière pendant une durée de 1/299 792 458 de seconde.
• Le kilogramme (kg), unité fondamentale de masse, est défini grâce à la valeur numérique de la constante de Planck $h = 6,62607015.10^{-34} kg.m^2.s^{-1}$, en ayant au préalable défini le mètre et la seconde.
• L’ampère (A), unité fondamentale d’intensité électrique, est défini en fixant la valeur numérique de la charge élémentaire $e=1,602176634.10^{-19} A.s$, en ayant défini au préalable la seconde.
• Le kelvin (K), unité fondamentale de température, est défini grâce à la valeur numérique de la constante de Boltzmann $k_B = 1,380649.10^{-23} kg.m^2.s^{-2}.K^{-1}$, en ayant au préalable défini le kilogramme, le mètre et la seconde.
• La mole (mol), unité fondamentale de quantité de matière, correspond à un nombre d’entités élémentaires égal à $N_A = 6,02214076 .10^{23} $, appelé nombre d’Avogadro.
• La candela (cd) est définie en se basant sur l’efficacité lumineuse d’un rayonnement monochromatique de fréquence 540 THz, $K_{cd}=683 cd.sr.kg^{-1}m^{-2}s^3$en ayant au préalable défini le kilogramme, le mètre et la seconde.

Grandeur	Symbole	Unité	Constante associée
Temps	$T$	seconde ($s$)	Fréquence de transition $\Delta \nu _{Cs} = 9,193.10^9 s^{-1}$
Longueur	$L$	mètre ($m$)	Vitesse de la lumière $c=3,00.10^8 m.s^{-1}$
Masse	$M$	kilogramme ($kg$)	Constante de Planck $h = 6,626.10^{-34} kg.m^2.s^{-1}$
Courant électrique	$I$	ampère ($A$)	Charge élémentaire $e = 1,602 . 10^{-19} A.s$
Température	$\Theta$	kelvin ($K$)	Constante de Boltzmann $k_B=1,381 .10^{-23} kg.m^2.s^{-2}.K^{-1}$
Quantité de matière	$N$	mole ($mol$)	$N_A=6,022.10^{23} mol^{-1}$
Intensité lumineuse	$J$	candela ($cd$)	Efficacité lumineuse $K_{cd}=683 cd.sr.kg^{-1}m^{-2}s^3$

Remarque : le nom d’une unité est un nom commun et s’écrit sans majuscule dans tous les cas (i.e. un kelvin). Lorsque l’unité est basée sur un nom propre, son symbole prend une majuscule (i.e. “$1073 K$ c’est un peu chaud pour le jacuzzi Kévin”). L’exception est le litre (i.e. “$2L$ de bière le jeudi ne te t’aideront pas pour le DS du vendredi”).

On rappelera que ces unités étaient initialement basées sur l’observation de phénomènes naturels (fraction du jour solaire, oscillation d’un pendule, …)

On peut déduire de ces unités fondamentales toutes les unités dérivées du système international (liste complète : https://en.wikipedia.org/wiki/SI_derived_unit). Par exemple, la capacité thermique s’exprime habituellement en $J.K^{-1}$, qui s’exprime dans le système fondamental : $kg.m^2.s^{-2}.K^{-1}$

Remarque : Dans beaucoup de domaines, on aura tendance a utiliser des unités dérivées pour un côté pratique. (voir les illustrations)

Exemple : Convertir les grandeurs des illustrations précédentes.

C. Préfixes multiplicatifs et puissances de dix

Il est pertinent dans la majorité des cas d’utiliser un préfixe d’unité afin d’éviter l’utilisation abusive et lourde des puissances de dix.

En pratique, il s’avère que dans beaucoup de domaines, les préfixes multiplicatifs seront utilisés par défaut :

• Spectroscopie : $nm$
• Distance en voiture : $km$
• Impulsions laser : $fs$
• Capacité de stockage informatique : $To$
• Puissance de calcul : pétaflops (FLoating point Operations Per Second)

Facteur	Nom	Symbole	Facteur	Nom	Symbole
$10^{1}$	déca	da	$10^{-1}$	déci	d
$10^{2}$	hecto	h	$10^{-2}$	centi	c
$10^{3}$	kilo	k	$10^{-3}$	milli	m
$10^{6}$	méga	M	$10^{-6}$	micro	$\mu$
$10^{9}$	giga	G	$10^{-9}$	nano	n
$10^{12}$	téra	T	$10^{-12}$	pico	p
$10^{15}$	péta	P	$10^{-15}$	femto	f

Remarque : Un angle n’a pas d’unité, le radian correspond à un ratio de longueurs (c’est par définition le quotient de la longueur d’un arc de cercle par le rayon).

D. Chiffres significatifs

Définition : Un chiffre significatif d’un nombre est :

• Tout chiffre non nul de ce nombre
• Tout “0” situé à droite d’un autre nombre

Lorsqu’on indique un nombre en physique, on indique en fait un encadrement de ce nombre. La précision de cet encadrement est directement reliée au nombre de chiffres significatifs.

Exemples :

• $x = 1.5$ signifie $1.45 \leq x < 1.55$
• $x = 1.500$ signifie $1.4995 \leq x < 1.5005$

Opérations :

• Le résultat d’une addition ou d’une soustraction a le même nombre de décimales que la donnée qui en possède le moins.
• Le résultat d’une multiplication ou d’une division a le même nombre de chiffre significatifs que la donnée qui en possède le moins.

E. Analyse dimensionnelle

Connaître les unités des grandeurs physiques que l’on manipule permet de vérifier la pertinence d’un calcul. En effet, une égalité entre deux membres implique nécessairement l’égalité des unités. Par conséquent, lors de tout calcul numérique, un élève avisé vérifiera systématiquement la cohérence des unités dans le calcul.

Exemple : (tiré d’un TD de cinématique) : On calcule une accélération grâce à la formule suivante : $a = \dfrac{v_0^2}{2 D}$ Vérifions la cohérence de cette équation :

On va chercher à déterminer l’unité du membre de droite, et vérifier si cela correspond bien à une accélération.

$[v] = L\times T^{-1}$ et $[D] = L$. De fait, le membre de droite est donc une grandeur de type $\dfrac{(L\times T^{-1})^2}{L}$et on obtient en simplifiant : $L\times T^{-2}$, ce qui correspond bien à une accélération.

F. Conversions

Un point rapide sur les conversions : afin d’éviter des erreurs de calcul on pourra utiliser la technique suivante :

$25 km/h = \dfrac{25 km}{1 h} = \dfrac{25 \times 1000 m}{1 \times 3600 s} = \dfrac{25}{3.6} m/s \simeq 6.9 m/s$

2. Dérivation des fonctions de la variable réelle

A. Définition

Soit $f$ une fonction définie sur $\mathbb{R}$ et $x_0 \in \mathbb{R}$ :

• $f$ est dite dérivable à droite en $x_0$ si : $ \lim\limits_{h \to 0^{+}} \dfrac{f(x_0+h)-f(x_0)}{h}$ est un nombre fini.

• $f$ est dite dérivable à gauche en $x_0$ si : $ \lim\limits_{h \to 0^{+}} \dfrac{f(x_0-h)-f(x_0)}{-h}$ est un nombre fini.

• $f$ est dite dérivable en $x_0$ si et seulement si elle est dérivable à droite et à gauche en $x_0$ et :

\[\lim\limits_{h \to 0^{+}} \dfrac{f(x_0+h)-f(x_0)}{h} = \lim\limits_{h \to 0^{+}} \dfrac{f(x_0-h)-f(x_0)}{-h} = \lim\limits_{h \to 0^{+}} \dfrac{f(x_0+h)-f(x_0-h)}{2h}\]

On appelle ces limites “dérivée de f en $x_0$” et elle se note $f’(x_0)$.

La fonction dérivée d’une fonction $f$ se note $f’$ et est définie pour tout point $x$ où $f$ est dérivable.

Exemple : La fonction $\begin{array}{rlll} f: \mathbb{R} & \longrightarrow & \mathbb{R} \ x & \longrightarrow & 3x^2+2 \end{array}$ est-elle dérivable en $x = 1$ ?

Calculons :

$\dfrac{f(1+h)-f(1)}{h} = \dfrac{3(1+h)^2 + 2 - (3*1^2 + 2)}{h} \newline = \dfrac{ 3(1+2h+h^2)+2-(3+2)}{h} = \dfrac{ 3+6h+3h^2+2-3-2}{h} \newline = \dfrac{6h + 3h^2}{h} = 6+3h \to_{h \to 0^{+}} 6$

En pratique : Il convient de savoir quelles sont les fonctions usuelles dérivables, et le cas échéant, quel est leur intervalle de dérivabilité, ainsi que la fonction dérivée associée ! (cf. méthodes, tableau de dérivation)

B. Détermination de l’équation de la tangente à une courbe

Le nombre dérivé d’une fonction en un point correspond au coefficient directeur de la tangente à la courbe représentative de la fonction en ce point.

En d’autres termes : soit la fonction $f$ que l’on va considérer dérivable sur $\mathbb{R}$ et admettant pour dérivée $f’$. Alors, en un point d’abcisse $a$ donnée, la tangente à la courbe $C_f$ représentative de la fonction $f$ a pour coefficient directeur $f’(a)$.

Plus précisément, la tangente a pour équation : $y = f’(a) * (x-a) + f(a)$

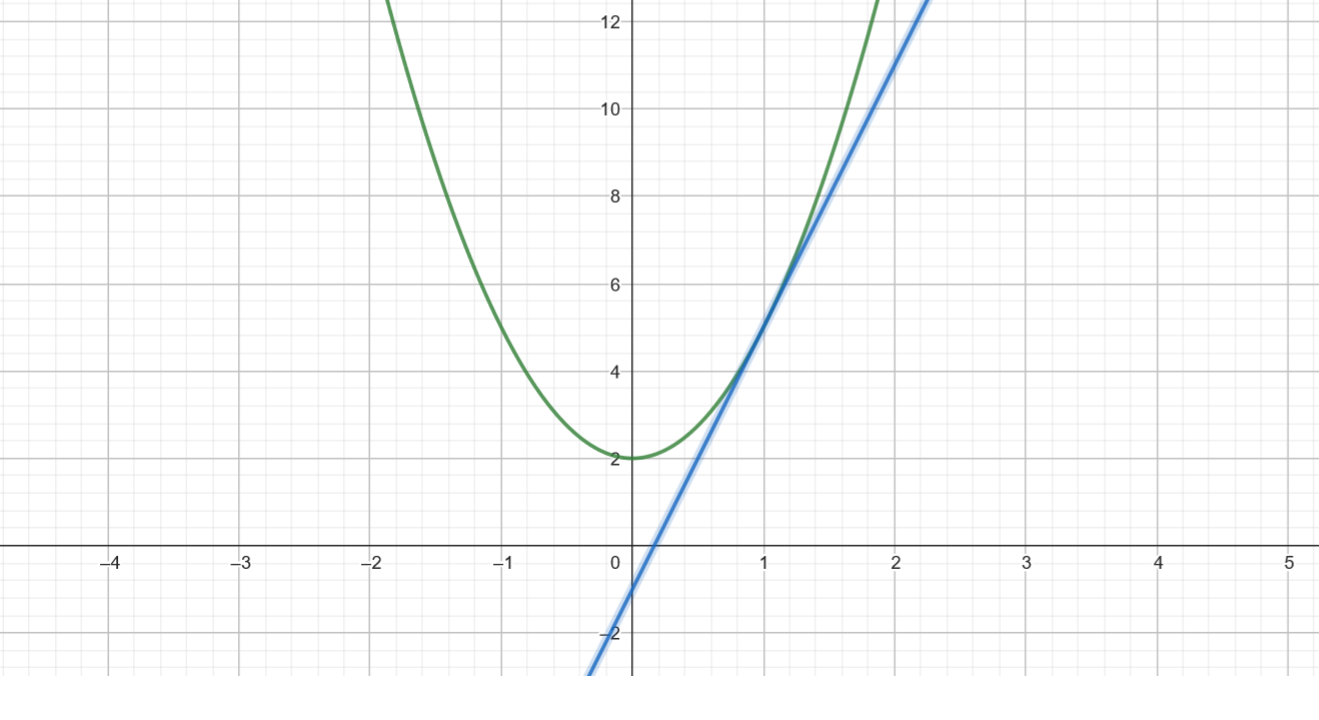
Exemple : Quelle est l’équation de la tangente à la fonction $f$ définie dans le paragraphe précédent, au point d’abcisse $x=1$ ?

On peut directement appliquer la formule ci-avant, afin de trouver : $y = 6(x-1) + 5 \iff y = 6x - 1$

C. Définition d’une dérivée seconde, dérivée $n$-ième

Si $f$ est dérivable deux fois, on appelle fonction dérivée seconde de $f$ la fonction dérivée de $f’$, que l’on notera $f’’$.

On peut généraliser cette définition de la manière suivante : si $f$ est dérivable $n$ fois, on appelle fonction dérivée $n$-ième de $f$ la fonction dérivée de $f’$, que l’on notera $f^{(n)}$.

3. Fonctions de plusieurs variables

A. Notation

Depuis tout petit, le lycéen considère les fonctions mathématiques comme des fonctions de la variable $x$, et prend l’habitude de noter $f’(x)$ le nombre dérivé de la fonction $f$ par rapport à la variable $x$. En revanche, le monde du physicien est autrement plus complexe. Nous sommes entourés de fonctions de plusieurs variables (on pourrait imaginer, par exemple, une modélisation de la température de la pièce en fonction de la température extérieure, du nombre d’individus présents, …). Le physicien a donc pour habitude d’indiquer en permanence la variable par rapport à laquelle il dérive une fonction, en utilisant la notation suivante : $\dfrac{df}{dx}$ représente la dérivée de la fonction $f$ par rapport à la variable $x$.

B. Dérivée partielle

Soit une fonction $(x,y) \longrightarrow f(x,y)$ à deux variables définie sur $\mathbb{R}^2$. La dérivée de la fonction $f$ par rapport à $x$ lorsque $y$ est constant est appelée dérivée partielle de $f$ par rapport à $x$ et se note :

$\left(\dfrac{\partial f(x,y)}{\partial x}\right)_{y = cst} \hspace{4mm}$ ou simplement $\hspace{4mm} \dfrac{\partial f}{\partial x}$

De même, la dérivée partielle de $f$ par rapport à $y$ se note :

$\left(\dfrac{\partial f(x,y)}{\partial y}\right)_{x = cst} \hspace{4mm}$ ou simplement $\hspace{4mm} \dfrac{\partial f}{\partial y}$

Exemple : $f(x,y) = 3x^2 + 2y^2$; $g(x,y) = 2xy^2$

• $\dfrac{\partial f}{\partial x} = 6x$; $\dfrac{\partial f}{\partial y} = 4y$
• $\dfrac{\partial g}{\partial x} = 2y^2$; $\dfrac{\partial g}{\partial y} = 4xy$

Remarque : On peut généraliser cette définition à une fonction d’un nombre quelconque de variables.

4. Mesures et incertitudes

A. Définitions

• Une mesurande est une grandeur physique que l’on mesure
• Un mesurage est une opération de mesure d’une mesurande. A la suite de cette opération, on obtient une valeur mesurée $x$ pour la mesurande.

Il est impossible de connaître la valeur exacte $x_{vrai}$ de la mesurande par les mesurages. Une mesure $x$ contient nécessairement une erreur $\varepsilon$ sur l’estimation de $x_{vrai}$ : $\varepsilon = x - x_{vrai}$

Cette erreur contient deux composantes :

• Erreur systématique : composante de l’erreur qui, dans des mesurages répétés, reste constante, ou varie de manière prévisible. (mauvais calibrage, approximation dans la modélisation…)
• Erreur aléatoire : composante de l’erreur qui, dans des mesurages répétés, varie de façon imprévisible. (précision des données des appareils de mesure, fluctuation des conditions expérimentales…)

B. Erreur aléatoire, évaluation de type A

On considère que l’on dispose, pour l’évaluation de $x_{vrai}$ d’une série de $n$ mesures indépendantes, $x_1, x_2, … x_n$

Dans l’évaluation de type A, $x_{vrai}$ est donnée par :

\[x_{vrai} = x_m \pm \dfrac{\sigma(x)}{\sqrt{n}}\]

avec : $x_m = \dfrac{1}{n} \sum\limits_{i} x_i$, la moyenne de la série de mesures,

et $\sigma(x) = \sqrt{\dfrac{1}{n}\sum\limits_{i} (x_i-x_m)^2}$ l’écart-type de la série de mesures.

L’évaluation de type A est une méthode statistique qui est d’autant plus précise que le nombre de mesures indépendantes $n$ est grande.

Remarque : il convient plutôt en physique de définir l’indicateur écart type en divisant par $n-1$ au lieu de $n$. L’indicateur indiqué ci-dessus est légèrement moins précis (discutable) mais s’aligne parfaitement avec la définition de l’écart-type mathématique pour éviter une confusion de la part de l’élève.

C. Evaluation de type B

Il s’agit maintenant de pouvoir évaluer l’erreur commise lors d’une mesure unique.

Mesure directe : Dans le cas d’une mesure directe, il existe généralement une précision $\Delta$ indiquée par l’appareil de mesure.

On peut considérer dans ce cas que $u(x) = \frac{\Delta}{\sqrt{3}}$ avec certaines considérations mathématiques (qui ne seront pas détaillés ici.) Cette relation sera notamment utile en TP lorsqu’il vous sera demandé d’évaluer

Mesure indirecte et composition des incertitudes :

Dans le cas d’une mesure indirecte, une valeur mesurée de la mesurande est déduite d’une formule mathématique faisant intervenir la mesure d’autres grandeurs $z_1, z_2, … z_n$ (appelées grandeurs d’entrée).

\[x = f(z_1, z_2, ... z_n)\]

On note $u_1, u_2, … u_n$ les incertitudes sur les grandeurs d’entrée. Si les grandeurs d’entrée sont indépendantes, alors l’incertitude $u(x)$ sur $x$ est donnée par :

\[u(x) = \sqrt{\left(\dfrac{\partial f}{\partial z_1}u_1\right)^2+\left(\dfrac{\partial f}{\partial z_2}u_2\right)^2+...+\left(\dfrac{\partial f}{\partial z_n}u_n\right)^2}\]

Exemple : On cherche l’énergie cinétique (et l’incertitude associée) d’une balle de ping pong, de masse $m = 2.7 \pm 0.1 g$ et de vitesse $v = 100 \pm 2 km/h$.

On commence par convertir les données dans le SI pour obtenir un résultat en $J$ : $m = 2.7\times 10^{-3} \pm 1\times 10^{-4} kg$, et $v = 27.8m/s \pm 0.56m/s$

$E_C = 1/2 m v ^2 = 1.0 J$

Pour le calcul de l’incertitude, on commence par calculer les dérivées partielles de $E_C$ : $\dfrac{\partial E_C}{\partial m} = \dfrac{1}{2} v^2$, et $\dfrac{\partial E_C}{\partial v} = mv$

On obtient pour l’incertitude totale :

$u(E_C) = \sqrt{\left(\frac{1}{2}v^2\times\Delta m\right)^2+\left(m v\times\Delta v\right)^2} \newline = \sqrt{(\frac{1}{2}\times 27.8^2 \times 10^{-4})^2 + (2.7 \times 10^{-3}\times 27.8 \times 0.56)^2} \newline =\sqrt{1.49\times 10^{-3} + 1.77\times 10^{-3}} \newline =5.7 \times 10^{-2} J$

On peut donner le résultat final sous la forme : $E_C = 1,0 \pm 0.06 J$, ou bien donner une incertitude relative sur le résultat : $\frac{u(E_C)}{E_C} = 0.06 = 6 \%$

More on units

https://www.youtube.com/watch?v=kkfIXUjkYqE