Chapitre 2 : Ondes
Qu’est-ce qu’un signal ?
Un signal physique correspond à l’évolution temporelle de la mesure d’une grandeur physique en un point donné de l’espace.
\[s(x,y,z,t)\]Toute grandeur physique dépendant du temps peut donc être considérée comme un signal : température, déplacement d’un point, pression, vitesse, tension […]
On peut bien évidemment observer des signaux unidimensionnels $s(x,t)$, qui seront les principaux sujets d’étude cette année.
Qu’est-ce qu’une onde ?
Exemples : Quels sont les ondes qui nous entourent ?
Cas de l’onde monochromatique
On va, pour simplifier l’étude, utiliser le cas d’une onde monochromatique pour introduire différents concepts.
La perturbation engendrée par une onde monochromatique présente une périodicité spatiale. C’est à dire, il existe une distance caractéristique $\lambda$ pour laquelle, $\forall x, \forall t, f(x+\lambda,t)=f(x,t)$
De même, cette perturbation présente également une périodicité temporelle : $\forall x, \forall t, f(x,t+T)=f(x,t)$
- $\lambda$ est appelée la longueur d’onde
- $T$ est appelée la période On définit également :
- $\sigma=\frac{1}{\lambda}$ le nombre d’onde
- $f=\frac{1}{T}$ la fréquence (temporelle)
Ces grandeurs spatiales et temporelles sont reliées entre elles par la célérité $c$ de l’onde : $\lambda = c T$
- $k=\frac{2\pi}{\lambda}$ la pulsation spatiale
- $\omega=2\pi f$ la pulsation temporelle
Notion de spectre
Sans aller dans le détail mathématique, on choisit d’étudier le cas d’une onde monochromatique car il s’avère que toute onde peut être décrite comme la superposition d’ondes monocrhomatiques. De ce fait, il est possible d’analyser une onde en termes des fréquences conetnues dans celle-ci : c’est une branche qu’on appelle l’analyse spectrale.
Remarque : l’analyse spectrale sera étudiée dans votre programme de mathématiques en 3ème année. On parlera notamment d’analyse de Fourier, un sujet au coeur de nombreuses innovations technologiques (genre, touts les algorithmes de compression du monde qui font que tu peux regarder cette vidéo sur ton téléphone sans trop te préoccuper de la bande passante : https://www.youtube.com/shorts/nXIHYB0Gp70 )
Dans le cadre de ce cours, il est simplement important de comprendre qu’il est à la fois possible de décrire une onde de manière temporelle, ou bien de manière spectrale.
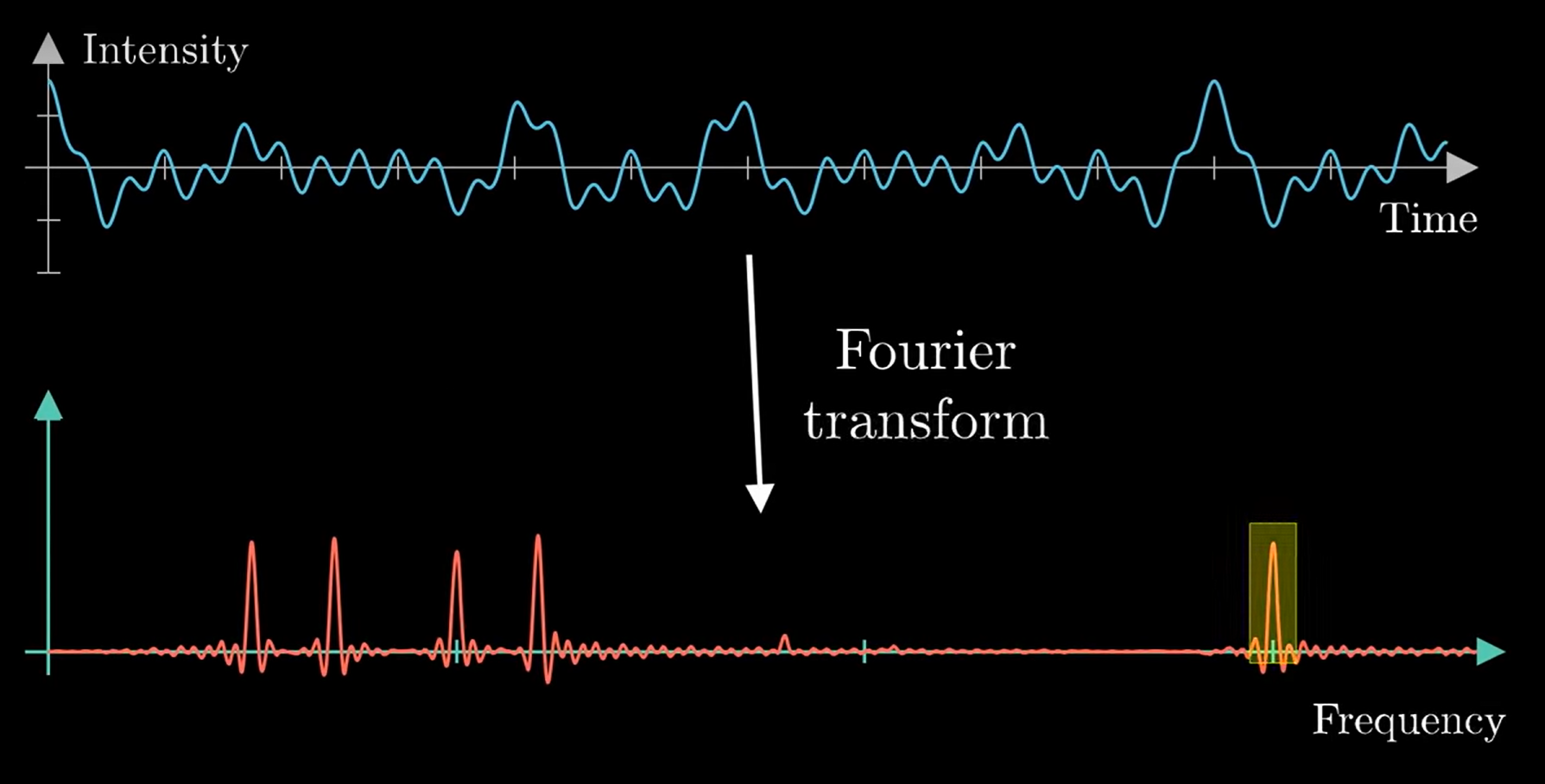
Source : https://www.youtube.com/watch?v=spUNpyF58BY&t=103s
Phénomène typiquement ondulatoires
Interférences
Lorsque deux ondes de même type se rencontrent et interagissent l’une avec l’autre, on observe un phénomène qu’on appelle d’interférence.
On distinguera :
- Les interférences constructives, qui apparaissent lorsque les amplitudes des ondes s’additionnent.
- Les interférences destructives, qui apparaissent lorsque les amplitudes des ondes s’annihilent.
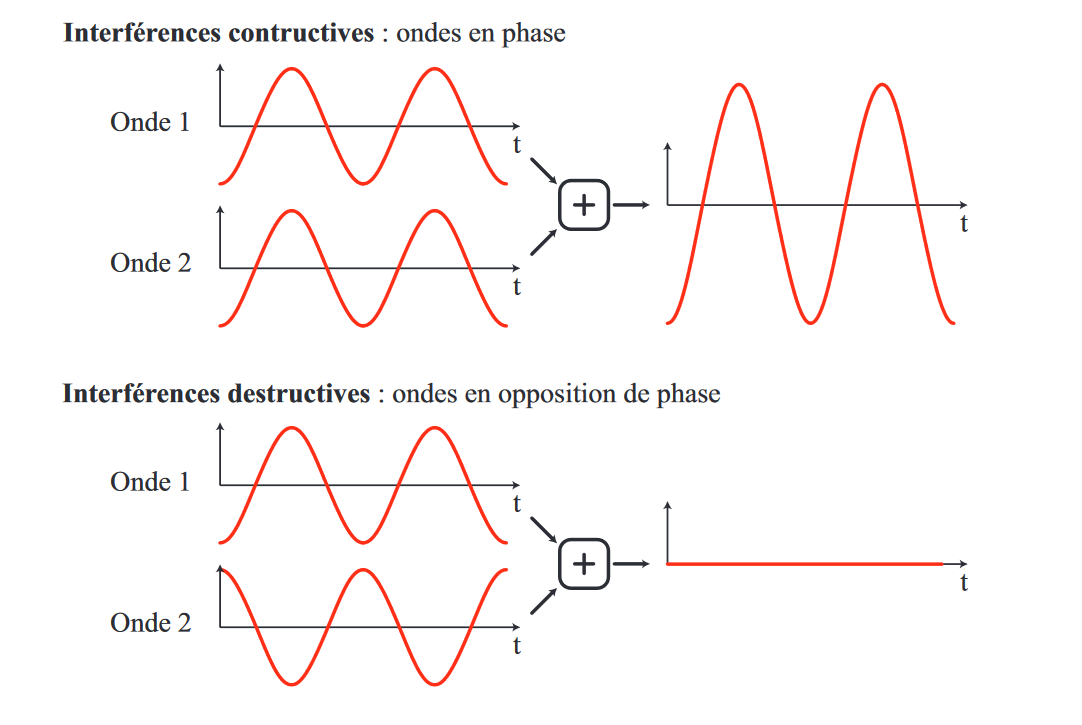
Quelques exemples :
- Casque à réduction de bruit active
- Exemple côté mécanique des fluides : https://youtu.be/Iuv6hY6zsd0?si=dfZc7TV2DiVFtIgM&t=278
- Interférences lumineuses : exemple de l’interféromètre de Michelson : https://en.wikipedia.org/wiki/Michelson_interferometer
Et à quoi ça sert ? : Concrètement, on utilise le plus souvent le phénomène d’interférence afin de mesurer précisément une distance. En effet, on peut atteindre une précision de l’ordre d’une fraction de la longueur d’onde. Et dans le cas des ondes lumineuses… ça fait une sacrée précision.
Calcul, et explication mathématique du phénomène :
Les calculs détaillés peuvent se trouver ici : https://www.etienne-thibierge.fr/cours-2024_optique/25_modele-scalaire_poly-prof.pdf
On va parler d’interférences constructives quand les deux ondes sont en phase : c’est à dire qu’elles présentent un déphasage $\Delta \phi = 2m\pi, m\in\mathbb{Z}$
On va parler d’interférences destructives quand les deux ondes sont en phase : c’est à dire qu’elles présentent un déphasage $\Delta \phi = (2m+1)\pi, m\in\mathbb{Z}$
Afin de simplifier l’étude de ce phénomène, on va plutôt raisonner en termes de différence de marche $\delta$. Cette distance $\delta$ correspond à la différence de chemin parcouru par les deux ondes.
Si $\delta = m\lambda, m\in\mathbb{Z}$, alors les intérférences sont constructives.
Si $\delta = (m+\frac{1}{2})\lambda, m\in\mathbb{Z}$, alors les intérférences sont destructives.
Dans les deux cas précédents, on appelle $m$ l’ordre d’intérférence.
Exercices-exemples :
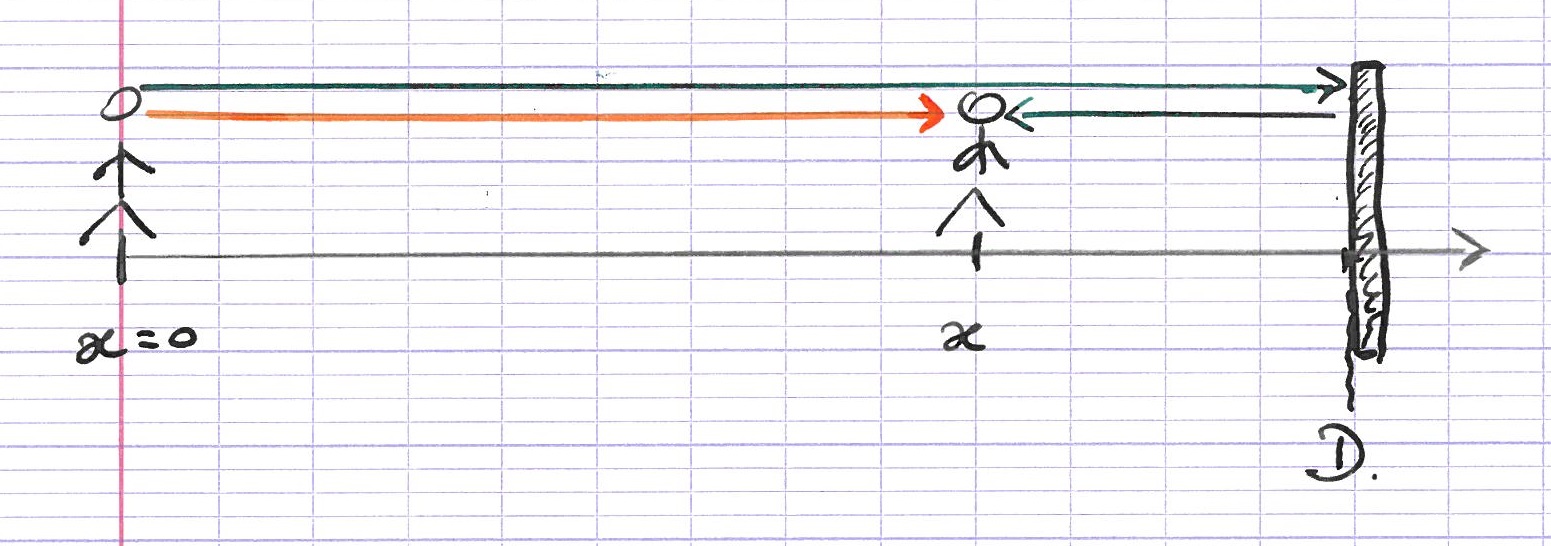
Un élève se place en $x=0$. Il émet une onde sonore de fréquence $f=20 Hz$ en direction des $x$ positifs. La vitesse de propagation d’une onde dans l’air est $c = 340 m.s^{-1}$. L’onde se réfléchit en $x=D$. On suppose qu’il n’y a aucune perte dûe à la propagation, ni à la réflexion. À quelle distance du mur son camarade doit-il se placer pour ne plus rien entendre ? Pour entendre du mieux possible ?
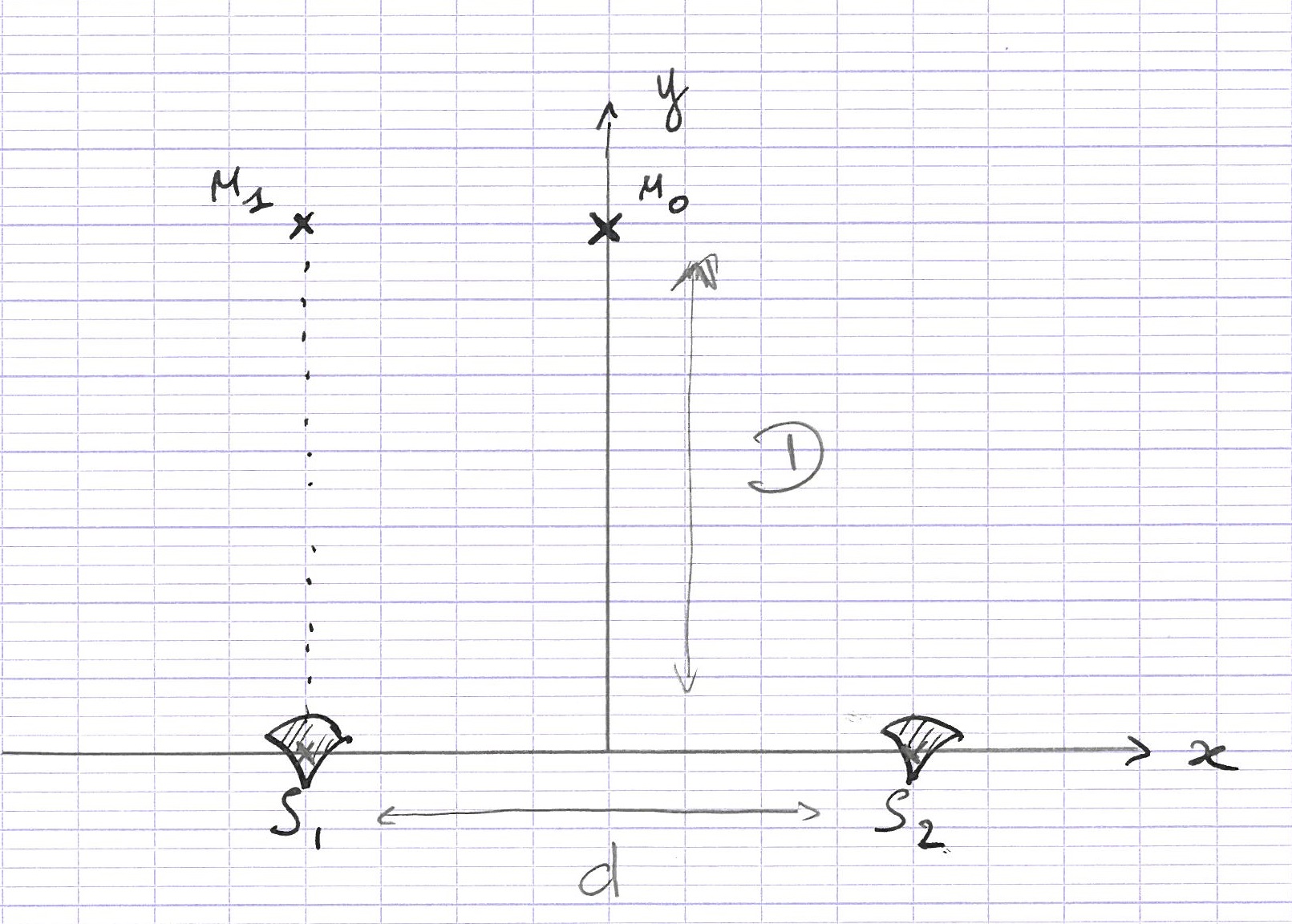
On considère deux haut-parleurs espacés de $d = 20 m$, qui émettent la même onde, cohérente, dans toutes les directions. Un auditeur se place en $M_0(0,D)$. Que dire des interférences en ce point ? L’auditeur se place désormais en $M_1$. Que dire des interférences en ce point ? Doit-il reculer ou avancer pour observer des intérférences constructives ? Destructives ?
Application numérique : $D = 30 m$, $f = 20 Hz$, $c = 340 m.s^{-1}$
Diffraction (hors programme)
Diffraction of water waves : https://www.youtube.com/watch?v=2TMR-EyF_ds