Chapitre 2 : Ondes - EXERCICES
Généralités sur les ondes
Exercice 1 :
On considère une onde unidimensionnelle se propageant sur l’axe $(Ox)$, modélisée par la fonction :
\[s(x,t) = 30 \times 10^3 \sin(60 \pi t - 5 \pi x +3 \pi)\]avec $s, x$ en $m$ et $t$ en $s$.
- Calculer la période, la fréquence, et la pulsation de ce signal.
- Calculer la longueur d’onde, le nombre d’onde, et le vecteur d’onde de ce signal
- Calculer l’amplitude de ce signal
Exercice 2 :
Quelle est la vitesse du son dans l’air à $20°C$ ?
Un jour d’orage, un observateur entend le tonnerre $3s$ après avoir vu l’éclair. Qu’en déduit-il ?
Exercice 3 :
La vitesse de propagation sur une corde tendue entre deux points $S_1$ et $S_2$, est $c = 10.0 m.s^{-1}$. La variation de l’élongation du point $S_1$ au cours du temps est représentée ci-après. Représenter, en supposant l’amortissement négligeable et une propagation verrs les $x$ croissants, l’aspect de la corde aux temps suivants : $0.010 s, 0.020 s, 0.030 s, 0.040 s$.
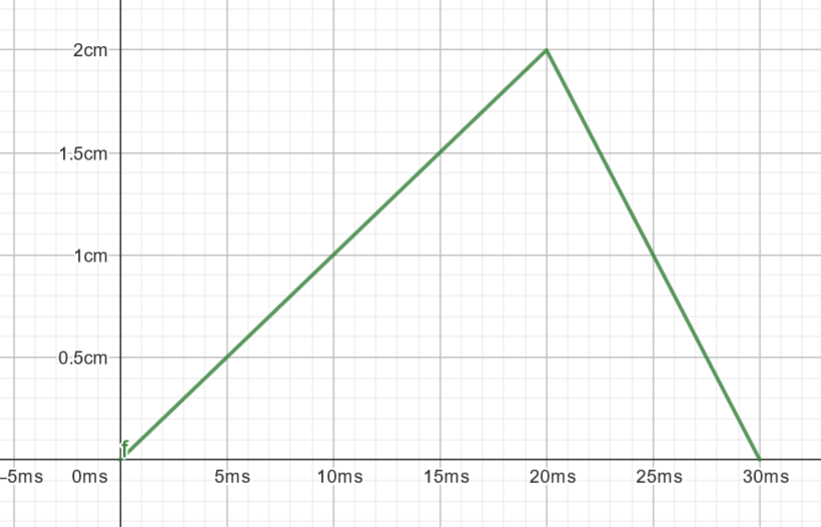
Bonus : le résultat est-il différent avec une forme d’excitation différente ?
Exercice 4 :
Un mascaret est une vague solitaire remontant un fleuve au voisinage de son estuaire, et provoquée par une interaction entre son écoulement et la marée montante. On considère un mascaret se propageant sans déformation le long d’une fleuve supposé rectiligne (on appelle ça un canal au pays des frites). On note $(Ox)$ l’axe de propagation de la vague. Un observateur placé en $x=0$ enregistre la hauteur de l’eau du fleuve en fonction du temps. Le résultat de cette mesure est donnée sur la figure suivante :
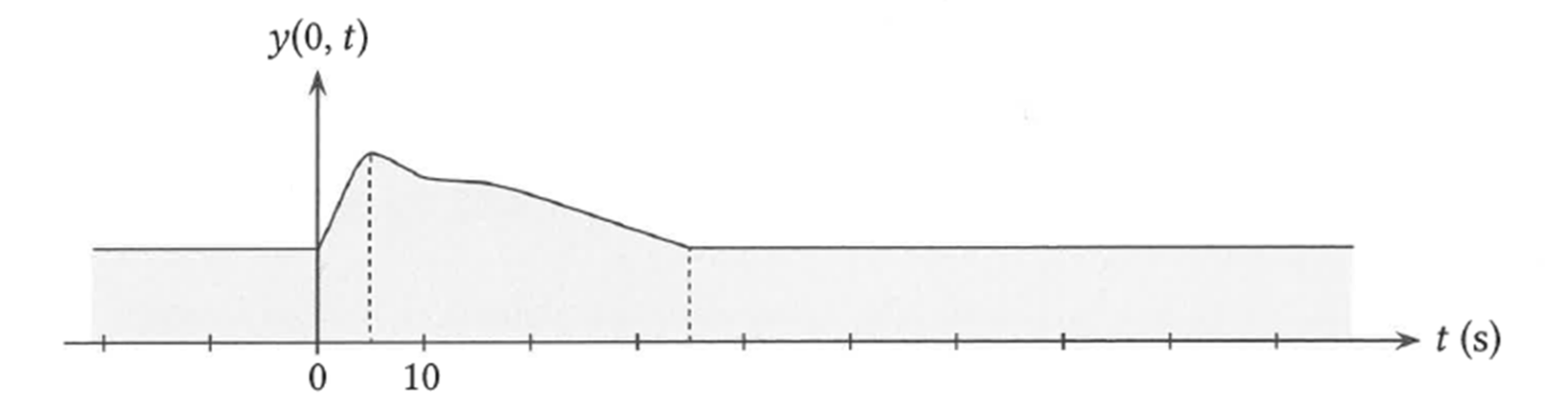
- Un deuxième observateur posté à une distance de $d = 500m$ du premier dans le sens de l’axe $(Ox)$ et ayant démarré son chronomètre au même instant voit le maximum de l’onde passer devant lui après une durée de $t_2 = 55s$. Déterminer la célérité du mascaret.
- Un batelier se trouve à l’abcisse $x_b = 1,4 km$, à quel instant la vague va-t-elle commencer à faire tanguer sa pirogue ?
- Un promeneur décide de prendre en photo le mascaret $20 s$ après que le premier observateur a vu le début de la vague. Représenter le profil spatial du mascaret vu sur la photo.
Une étude approfondie du phénomène permet de montrer que : \(y(x,t) = H +\dfrac{A}{\cosh\left(\sqrt{\dfrac{3A}{4H^2}\left(x-\sqrt{gH}\left(1 + \dfrac{A}{2H}\right)t\right)}\right)}\)
où $g$ est l’accélération de la pesanteur, $H$ la hauteur d’eau avant et après le passage de l’onde, et $A$ l’amplitude de l’onde. $\cosh$ est une fonction mathématique qu’il n’est pas nécessaire de connaître (même si elle est gravement stylée)
- À partir de l’expression de $y(x,t)$, identifier l’expression de la célérité de l’onde. De quels paramètres dépend-elle ?
- En réalité, l’onde se déforme petit à petit car la vitesse de propagation augmente avec la profondeur. Comment évolue le profil de la vague ?
- En termes d’ordre de grandeur, le club RunISEN peut-il rivaliser avec la vitesse du mascaret ? Qu’en est-il de Mr COLIN à vélo ?
Interférences
Exercice 5 :
Un tachéomètre est un instrument de mesure de distance utilisé par les géomètres pour effectuer un bornage. Lors de cette mersure, une onde électromagnétique de fréquence $f_1 = 30 000 kHz$ est émise par l’instrument, cette onde se réfléchit sur un réflecteur placé à une distance $d$ du géomètre. La mesure du déphasage entre l’onde émise et l’onde reçue permet de déterminer la distance $d$. L’indice de l’air à température ambiante est $n_a = 1.00029$ et la célérité des ondes électromagnétiques dans le vide est $c = 2.99792 \times 10^8 m.s^{-1}$. La fréquence $f_1$ est connue avec une précision relative de $10^{-5}$.
La figure ci-dessous représente les signaux emis et reçu par le tachéomètre.
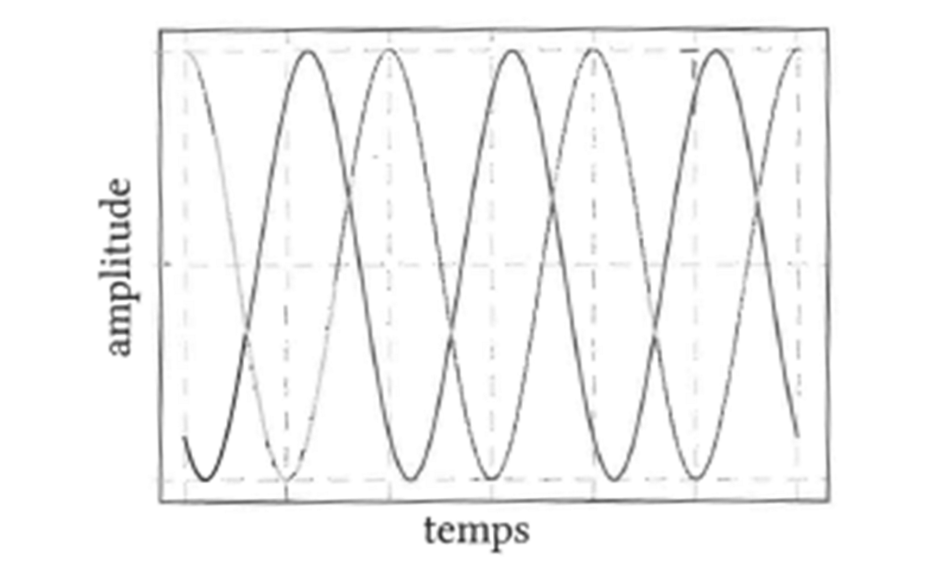
- Exprimer le déphasage $\Delta \varphi_{e/r}$ de l’onde émise par rapport à l’onde reçue en fonction de $d, f_1, c$, et $n_a$.
- On note $\tau$ le retard du signal reçu dû à la propagation et $T_1 = 1/f_1$ la période du signal. À partir de la figure, mesurer le rapport $\tau / T_1$ ainsi que son incertitude associée.
- En déduire une estimation $d_0$ de la distance $d$ séparant le tachéomètre et le réflecteur.
- Quelle distance $d_{max}$ peut être mesurée sans ambiguïté par cette méthode ?