Chapitre 3 : Fondements de l’électrocinétique
1. Notions de base
Le terme électrocinétique renvoie à l’ensemble des phénomènes et des lois relatifs aux charges électriques en mouvement.
A. Charge électrique
La charge électrique, notée $q$, caractérise la capacité de la matière à interagir par des champs électromagnétiques (on peut considérer que c’est une grandeur analogue à la masse, à la différence près qu’une charge électrique peut être négative). La charge électrique est quantifiée, avec une quantité élémentaire : $e = 1,6\times 10^{-19} C$. Ceci correspond à la charge d’un proton, ou celle d’un électron (à un signe près).
B. Courant électrique
Le courant électrique, généralement noté $i$, correspond lui à un mouvement de charges électriques. On peut le décrire comme étant le débit de charge électrique, c’est à dire : $i(t) = \frac{dq}{dt}$.
Il existe différents types de porteurs de charges. Typiquement, dans les fils électriques, les porteurs de charges sont les électrons. Dans des solutions aqueuses, les porteurs de charges sont des ions.
Ordres de grandeur des courants électriques :
| Intensité électrique | Phénomène / dispositif correspondant |
|---|---|
| $10mA$ | LED |
| $100mA$ | Début de risque d’électrocution* |
| $1 A$ | Ampoule à incandescence |
| $10 A$ | Radiateur électrique |
| $100 A$ | Démarreur automobile |
| $500 A$ | Moteur de locomotive TGV |
| $1 kA$ | Lignes à haute tension |
| $10 - 100 kA$ | Éclairs orageux |
*Un courant alternatif de $75mA$ à $50 Hz$ pendant une seconde produit une fibrillation ventriculaire.
C. Potentiel électrique
Le potentiel électrique est intimement lié à la notion de champ électrique. Pour comprendre ce dernier, il peut être utile d’utiliser une analogie avec le champ gravitationnel.
Analogie charge-masse, champ électrique-gravitationnel
Tout corps de masse $M$ produit autour de lui une force d’attraction sur tout objet de masse $m$ dans son environnement, définie par :
\[\vec{F} = -\dfrac{GMm}{r^2}\vec{u_r}\]On peut écrire cette relation sous la forme :
\[\vec{F} = m \times \left(-\dfrac{GM}{r^2}\vec{u_r}\right)\]Et on retrouve la relation bien connue des lycéens : $\vec{F} = m \vec{g}$ (dans le cas d’un objet à la surface de la Terre, notamment)
Or, en fonction de la distance du corps de masse $m$ à celui de masse $M$, on sait que la valeur de $\vec{g}$ peut varier. En fait, $\vec{g}$ est différent en tout point de l’espace. Plus on s’éloigne, plus sa valeur diminue. De plus, sa direction est toujours en direction du corps de masse $M$.
On vient de définir un champ vectoriel, c’est à dire une fonction vectorielle, qui prend une valeur dépendant de la position où on la considère.
Quelques exemples d’autres champs :
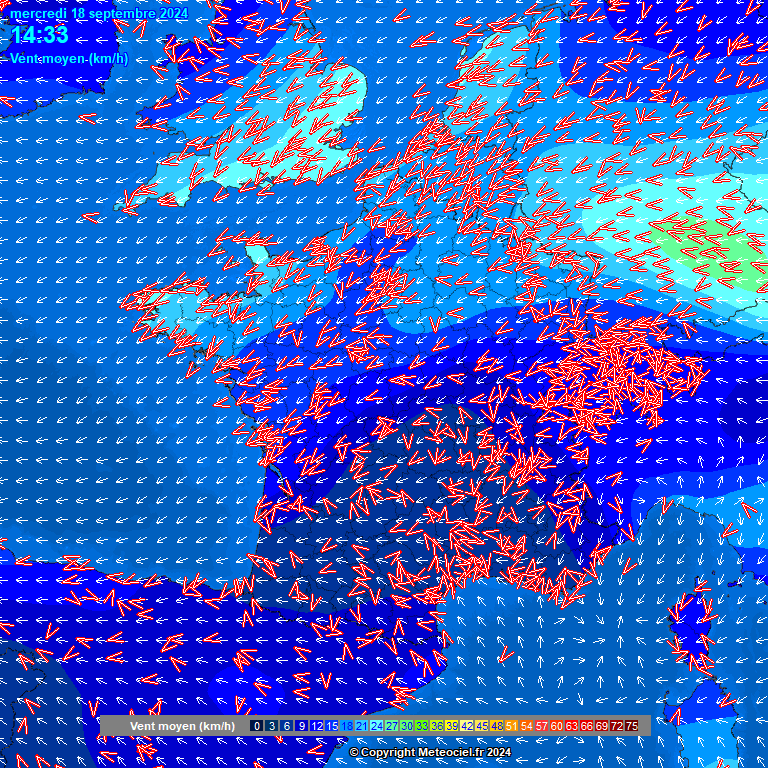
- Une carte des vents (champ vectoriel)
- Une carte de la température (champ scalaire)
 |
 |
Pour terminer notre analogie, on va considérer que le champ électrique se comporte comme le champ gravitationnel. Dans le cas gravitationnel, on considère que les masses vont avoir tendance à se déplacer depuis les potentiels élevés (c’est à dire les altitudes élevées) vers les potentiels faibles. De la même manière, les charges électriques positives vont avoir tendance à se déplacer des potentiels électriques élevés vers les potentiels électriques faibles.
On définit également une tension électrique comme étant la différence de potentiel électrique entre deux points. En pratique, on va définir le potentiel électrique en tout point d’un circuit, et la tension électrique correspondra à la différence entre deux points considérés.
On définit la masse d’un circuit comme étant le point avec un potentiel électrique $V =0$.
D. Analogie complète eau / charge
| Électrocinétique | Gravitation - eau |
|---|---|
| Charge positive | Goutte d’eau |
| Champ électrique $\vec{E}$ | Champ gravitationnel $\vec{g}$ |
| Potentiel électrique | Altitude |
| Tension | Dénivelé |
| Courant électrique | Débit |
2. Dipôle récepteur / générateur
Définition
Un dipôle est un élément relié au circuit par deux bornes. On va considérer deux types de dipôles principaux :
- Les dipôles générateurs (une pile par exemple)
- Les dipôles récepteurs (une résistance par exemple)
Dans un dipôle générateur, on oriente par convention l’intensité et la tension dans le même sens. De plus, ces deux grandeurs permettent de calculer la puissance fournie par le dipôle : $P = U\times I$
Dans un dipôle récepteur, on oriente par convention l’intensité et la tension dans des sens opposés. De plus, ces deux grandeurs permettent de calculer la puissance reçue par le dipôle : $P = U\times I$
Loi d’Ohm
Dans une résistance, il existe une relation linéaire entre la tension aux bornes du dipôle, et le courant qui le traverse : $U = R\times I$
Exercice : Comment exprimer la puissance reçue par une résistance ?
3. Lois de Kirchhoff
A. Loi des noeuds
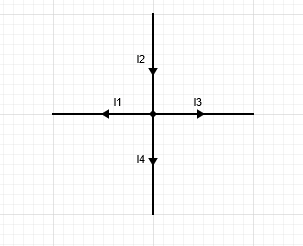
- La somme algébrique des courants entrant un noeud est nulle.
ou
- Le somme des courants entrant un noeud est égale à la somme des courants sortants.
Ici, $I_2-I_1-I_3-I_4 = 0$, ou encore $I_2 = I_1+I_3+I_4$
B. Loi des mailles
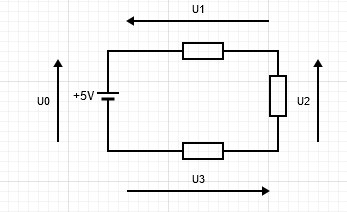
- La somme algébrique des tensions autour d’une boucle est nulle.
Ici, $U_0-U_1-U_2-U_3=0$
C. Théorème de Millmann
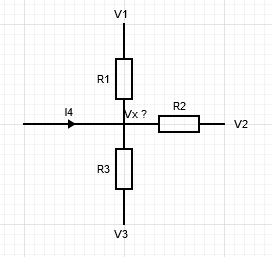
Le théorème de Millmann combine les deux lois précédentes, et permet de grandes simplifications dans les calculs.
\[V_x = \dfrac{\dfrac{V_1}{R_1}+\dfrac{V_2}{R_2}+\dfrac{V_3}{R_3}+I_4}{\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}}\]4. Association de résistances
A. Association de résistances en série
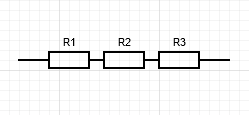
$R_{eq} = R_1 + R_2 + R_3$
Lorsqu’on associe des résistances en série, on rend le passage du courant plus difficile, donc on additionne les résistances.
Formule du diviseur de tension :
Si on considère deux résistances en série :
$U_1 = \dfrac{U_{total} \times R_1}{R_1+R_2}$, $U_2 = \dfrac{U_{total} \times R_2}{R_1+R_2}$
B. Association de résistances en parallèle
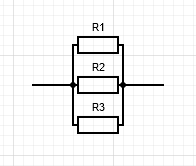
$\dfrac{1}{R_{eq}} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3}$
Lorsqu’on associe des résistances en parallèle, on rend le passage du courant plus facile, donc on additionne les conductances ($G = \frac{1}{R}$).
Formule du diviseur de courant :
Si on considère deux résistances en parallèle :
$i_1 = \dfrac{i_{total} \times R_2}{R_1+R_2}$, $i_2 = \dfrac{i_{total} \times R_1}{R_1+R_2}$