Chapitre 4 : Régimes transitoires dans les circuits linéaires du premier ordre
1. Notions de base
A. Régime permanent
“En physique, un régime permanent est le régime d’un système stable qui peut être observé après un certain temps, lorsque le régime transitoire est terminé.”
(Wikipédia)
B. Régime stationnaire
Le régime stationnaire est un cas particulier du régime permanent, où les tensions et les intensités sont indépendants du temps.
(On verra un autre cas particulier de régime permanent, le régime permanent sinusoïdal)
C. Régime transitoire
“En physique, un régime transitoire est le régime d’évolution d’un système qui n’a pas encore atteint un état stable (un régime permanent).”
(Wikipédia)
En électronique, on peut rencontrer ce genre de régime transitoire typiquement à l’ouverture / fermeture d’un interrupteur.
Dans ce chapitre, on va étudier les régimes transitoires dits du premier ordre.
Nous allons étudier ce phénomène à travers un exemple simple et courant : la charge et la décharge d’un condensateur.
2. Charge et décharge d’un condensateur
A. Condensateur
Un condensateur est un dipôle électrique, composé de deux armatures conductrices, séparées par un isolant (appelé diélectrique)
Il présente la propriété de pouvoir stocker des charges électriques contraires sur ses armatures. Cette propriété est caractérisée par sa capacité électrique $C$, exprimée en farads ($F$).
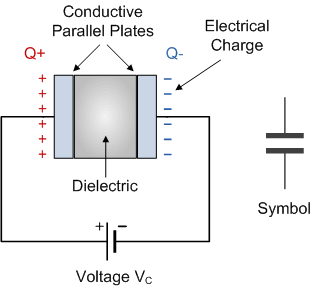
Le courant électrique, généralement noté $i$, correspond lui à un mouvement de charges électriques. On peut le décrire comme étant le débit de charge électrique, c’est à dire : $i(t) = \frac{dq}{dt}$.
Le courant dans un condensateur est donc créé lorsque les charges sont en cours d’accumulation (ou de déplétion) sur les armatures. La relation caractéristique du condensateur s’écrit : \(i_C(t) = C \dfrac{du_C}{dt}\)
En d’autres termes, il existe un courant électrique dans le condensateur lorsqu’il existe une modification de la tension du condensateur.
En pratique, on peut relier la charge du condensateur à sa tension en remarquant :
\[i_C(t) = \dfrac{dq_C}{dt} = C \dfrac{du_C}{dt}\] \[\Leftrightarrow q_C(t) = C u_C(t)\]B. Circuit RC série et charge d’un condensateur
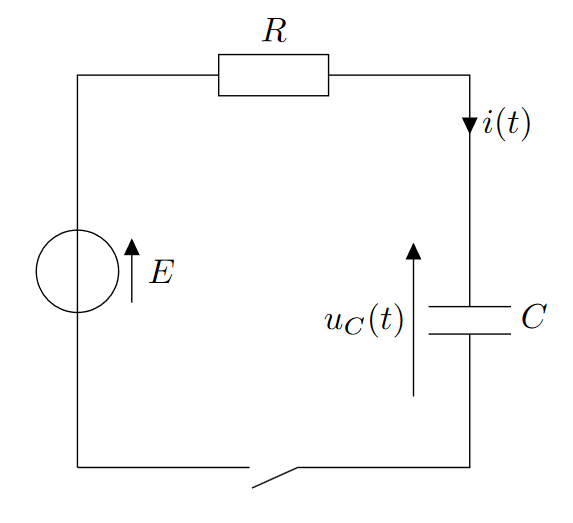
- À $t < 0$, on considère que le condensateur est déchargé, et que l’interrupteur est ouvert $\Rightarrow u_C = 0$ et $i=0$.
- À $t=0$, on ferme l’interrupteur (le condensateur va donc commencer à se charger)
On cherche maintenant à déterminer le comportement du circuit pour $t\geq0$
Pour ce faire, nous allons chercher à déterminer $u_C(t)$, en trois étapes :
- Écrire les équations caractéristiques du circuit (mailles, noeuds, composants)
- Établir l’équation différentielle vérifiée par $u_C(t)$
- Résoudre l’équation différentielle
Remarque : Ces étapes s’appliquent à l’étude de tout circuit pour ce chapitre !
Équations caractéristiques du circuit
- Loi des mailles : $(1) : E = u_C(t) + u_R(t)$
- Loi d’Ohm : $(2) : u_R(t) = R.i(t)$
- Loi du condensateur : $(3) : i(t) = C \dfrac{du_C}{dt}$
On va maintenant combiner ces trois équations afin d’obtenir une équation unique qui ne contient que $u_C(t)$.
Remarque : Cette démarche sera toujours possible lorsqu’on a autant d’équations que d’inconnues (et que les équations sont indépendantes, cf. cours de maths). Ici on a trois équations pour trois inconnues : $u_R(t), u_C(t), i(t)$.
Équation différentielle en $u_C(t)$
$(3) : i(t) = C \dfrac{du_C}{dt}$
On élimine $i(t)$ en utilisant $(2) : i(t) = \dfrac{u_R(t)}{R}$
$\Leftrightarrow \dfrac{u_R(t)}{R} = C \dfrac{du_C}{dt}$
On élimine $u_R(t)$ en utilisant $(1) : u_R(t) = E - u_C(t)$
$\Leftrightarrow \dfrac{E - u_C(t)}{R} = C \dfrac{du_C}{dt}$
Il ne reste qu’à remettre en forme l’équation :
$\Leftrightarrow \dfrac{E}{R} - \dfrac{u_C(t)}{R} = C \dfrac{du_C}{dt}$
$\Leftrightarrow \boxed{\dfrac{E}{RC} = \dfrac{du_C}{dt} +\dfrac{u_C(t)}{RC}}$
On obtient ainsi une équation différentielle linéaire du premier ordre à coefficients réels constants.
- Équation différentielle : l’inconnue est une fonction, et l’équation est une relation entre la fonction et ses dérivées.
- Linéaire : pas de $f^2$
- Premier ordre : uniquement des dérivées d’ordre 1 ($f’, \cancel{f’’}$)
- On a ici écrit l’équation sous forme canonique, c’est à dire que le coefficient devant la dérivée de plus haut ordre est $1$.
- On appelle second membre le terme constant dans l’équation différentielle (ici $\frac{E}{RC}$)
Résolution de l’équation différentielle
Remarque : la méthode détaillée ici sera utilisée pour toutes les équations différentielles d’ordre $1$.
La résolution se déroule en trois étapes :
- Solution particulière
- Solution homogène
- Détermination des constantes grâce aux conditions intiales
- Solution particulière $u_{C,p}(t)$:
On cherche la solution en régime permanent. On sait que lorsque la charge du condensateur sera terminée, on aura $\frac{du_C}{dt} = 0$. L’équation devient alors : \(\dfrac{1}{RC} u_{C,p}(t) = \dfrac{E}{RC}\) \(\Leftrightarrow \boxed {u_{C,p}(t) = E}\)
- Solution homogène $u_{C,h}(t)$:
On écrit l’équation dite “sans second membre”, c’est à dire qu’on écrit l’équation sans les termes qui ne dépendent pas de $u_C(t)$ : \(\dfrac{du_{C,h}}{dt} + \dfrac{1}{RC} u_{C,h}(t) = 0\)
Théorème : L’équation $y’(t) + a.y(t) = 0$ a pour solution : $y(t) = \alpha e^{-at}$ où $\alpha$ est une constante à déterminer.
Donc ici, on peut en déduire que $\boxed{u_{C,h}(t) = \alpha e^{-\frac{t}{RC}}}$
- Conclusion (et détermination de la constante $\alpha$) :
La solution complète de l’équation différentielle est :
\[u_C(t) = u_{C,p}(t) + u_{C,h}(t) = E + \alpha e^{-\frac{t}{RC}}\]Il faut déterminer $\alpha$ afin de terminer la résolution. Pour ce faire, on doit utiliser une condition intiale qui donne la valeur de $u_C(t)$ à un temps donné. Ici, on sait que $u_C(t=0) = 0$.
Alors, \(u_C(t=0) = 0\) \(\Leftrightarrow E + \alpha e^{-\frac{0}{RC}} = 0\) \(\Leftrightarrow E + \alpha \times 1 = 0\) \(\Leftrightarrow \alpha = -E\)
Et on peut donc finalement écrire que : \(u_C(t) = E - E e^{-\frac{t}{RC}}\)
ou encore :
\[\boxed{u_{C}(t) = E\left(1 - e^{-\frac{t}{RC}}\right)}\]Tracé de la courbe :
On peut faire plusieurs remarques sur cette courbe :
- On retrouve bien la valeur $u_C(t\to\infty) = E$
- Il existe plusieurs valeurs remarquables : $u_C(RC) \simeq 0.63E$, $u_C(3.RC) \simeq 0.95E$, $u_C(5.RC) \simeq 0.99E$
- On pourra généralement que le condensateur est complètement chargé après $5.RC$
Intensité dans le condensateur :
Une fois le calcul de la tension dans le condensateur effectué, il est assez simple d’accéder à la valeur de l’intensité en utilisant la formule de base : $i(t) = C \dfrac{du_C}{dt}$
On obtient alors : $i(t) = \dfrac{E}{R} e^{-\frac{t}{RC}}$
Remarque importante :
L’intensité dans le condensateur est nulle à $t<0$. Or, d’après la formule ci-dessus, $i(t = 0^+) = E/R$. Il y a donc une discontinuité de l’intensité dans le condensateur au moment ou la charge débute !
C. Décharge du condensateur :
On considère désormais que le condensateur est chargé, et qu’on éteint le générateur à $t=0$.
On peut modéliser cette expérience par le circuit ci-dessous :
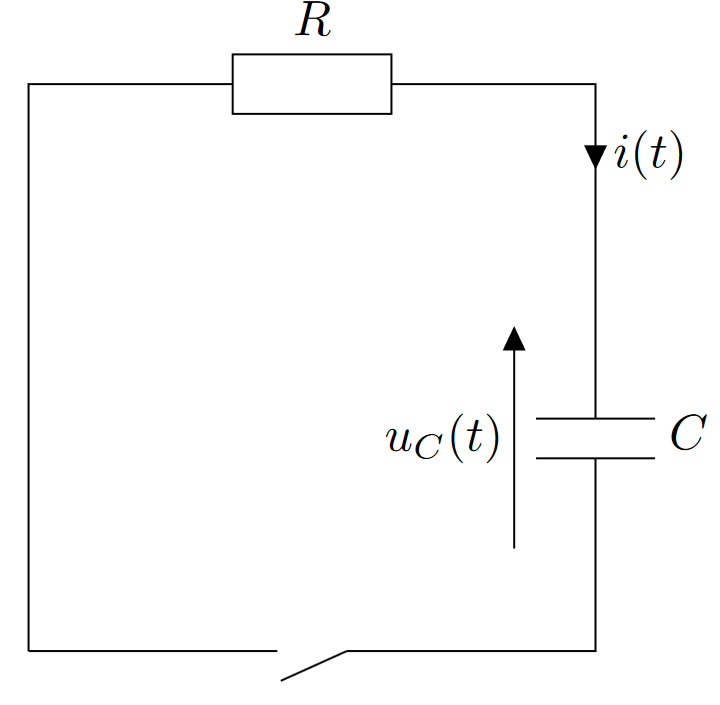
- À $t < 0$, on considère que le condensateur est chargé, et que l’interrupteur est ouvert $\Rightarrow u_C = E$ et $i=0$.
- À $t=0$, on ferme l’interrupteur (le condensateur va donc commencer à se décharger)
On cherche maintenant à déterminer le comportement du circuit pour $t\geq0$
Équations caractéristiques du circuit
- Loi des mailles : $(1) : 0 = u_C(t) + u_R(t)$
- Loi d’Ohm : $(2) : u_R(t) = R.i(t)$
- Loi du condensateur : $(3) : i(t) = C \dfrac{du_C}{dt}$
On va maintenant combiner ces trois équations afin d’obtenir une équation unique qui ne contient que $u_C(t)$.
Équation différentielle en $u_C(t)$
$(3) : i(t) = C \dfrac{du_C}{dt}$
On élimine $i(t)$ en utilisant $(2) : i(t) = \dfrac{u_R(t)}{R}$
$\Leftrightarrow \dfrac{u_R(t)}{R} = C \dfrac{du_C}{dt}$
On élimine $u_R(t)$ en utilisant $(1) : u_R(t) = - u_C(t)$
$\Leftrightarrow \dfrac{- u_C(t)}{R} = C \dfrac{du_C}{dt}$
Il ne reste qu’à remettre en forme l’équation :
$\Leftrightarrow \boxed{\dfrac{du_C}{dt} +\dfrac{u_C(t)}{RC} = 0}$
Résolution de l’équation différentielle
- Solution particulière $u_{C,p}(t)$:
On cherche la solution en régime permanent. On sait que lorsque la charge du condensateur sera terminée, on aura $\frac{du_C}{dt} = 0$. L’équation devient alors : \(\dfrac{1}{RC} u_{C,p}(t) = 0\) \(\Leftrightarrow \boxed {u_{C,p}(t) = 0}\)
- Solution homogène $u_{C,h}(t)$:
Remarque : Ici l’équation sans second membre est donc la même que l’équation de base !
On écrit l’équation dite “sans second membre”, c’est à dire qu’on écrit l’équation sans les termes qui ne dépendent pas de $u_C(t)$ : \(\dfrac{du_{C,h}}{dt} + \dfrac{1}{RC} u_{C,h}(t) = 0\)
Théorème : L’équation $y’(t) + a.y(t) = 0$ a pour solution : $y(t) = \alpha e^{-at}$ où $\alpha$ est une constante à déterminer.
Donc ici, on peut en déduire que $\boxed{u_{C,h}(t) = \alpha e^{-\frac{t}{RC}}}$
- Conclusion (et détermination de la constante $\alpha$) :
La solution complète de l’équation différentielle est :
\[u_C(t) = u_{C,p}(t) + u_{C,h}(t) = 0 + \alpha e^{-\frac{t}{RC}}\]Il faut déterminer $\alpha$ afin de terminer la résolution. Pour ce faire, on doit utiliser une condition intiale qui donne la valeur de $u_C(t)$ à un temps donné. Ici, on sait que $u_C(t=0) = E$.
Alors, \(u_C(t=0) = E\) \(\Leftrightarrow \alpha e^{-\frac{0}{RC}} = E\) \(\Leftrightarrow \alpha = E\)
Et on peut donc finalement écrire que :
\[\boxed{u_{C}(t) = Ee^{-\frac{t}{RC}}}\]Tracé de la courbe :
D. Exercice d’application :
On considère le circuit suivant :

- À $t < 0$, on considère que le condensateur est déchargé, et que l’interrupteur est ouvert.
- À $t=0$, on ferme l’interrupteur.
- Que vaut $u_C(t=0)$?
- Déterminer $u_C(t)$ pour $t>0$.
- Une fois le régime permanent atteint dans la situation précédente, on rouvre l’interrupteur. On choisit comme nouvelle origine des temps cet instant. Donner la nouvelle expression de $u_C(t)$.
SOLUTION :
Il est de bon usage de commencer par annoter tout le circuit :
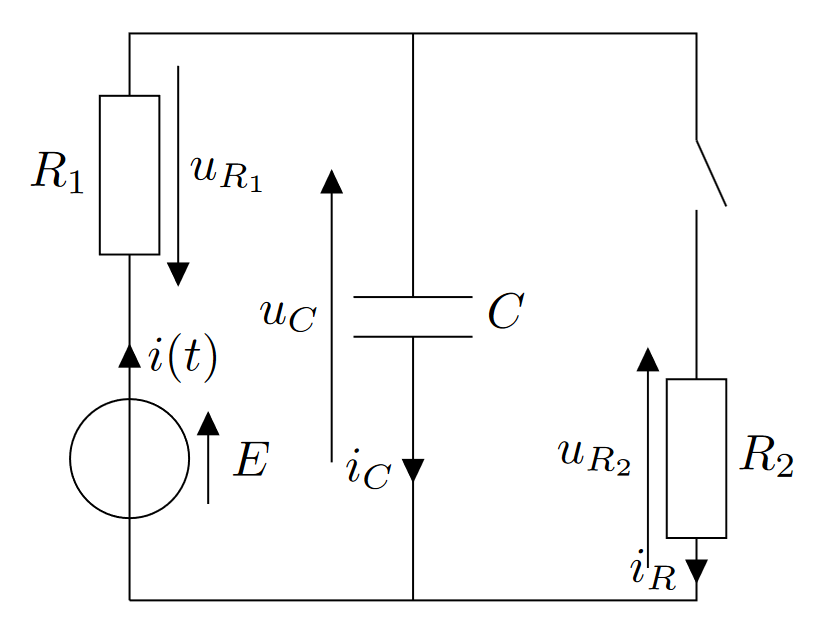
-
Le condensateur étant déchargé à $t=0$, on peut dire que $u_C(t=0)=0$.
-
On fait tout d’abord l’inventaire des équations caractéristiques du circuit :
- $(1)$ Loi des mailles : $E - u_{R_1}(t) - u_{R_2}(t) = 0$
- $(2)$ Loi des mailles : $u_{R_2}(t) = u_C(t)$
- $(3)$ Loi des noeuds : $i(t) = i_C(t) + i_R(t)$
- $(4)$ Loi d’Ohm : $u_{R_1}(t) = R_1 . i(t)$
- $(5)$ Loi d’Ohm : $u_{R_2}(t) = R_2 . i_R(t)$
- $(6)$ Loi du condensateur : $i_{C}(t) = C \dfrac{du_C}{dt}$
On remplace $i_C(t)$ en utilisant $(3) : i_C(t) = i(t) - i_R(t)$
\[\Leftrightarrow i(t) - i_R(t) = C \dfrac{du_C}{dt}\]On remplace $i(t)$ et $i_R(t)$ en utilisant $(4, 5) : i(t) = \dfrac{u_{R_1}(t)}{R_1}, i_R(t)= \dfrac{u_{R_2}(t)}{R_2}$
\[\Leftrightarrow \dfrac{u_{R_1}(t)}{R_1} - \dfrac{u_{R_2}(t)}{R_2} = C \dfrac{du_C}{dt}\]On remplace $u_{R_1}(t)$ et $u_{R_2}(t)$ en utilisant $(1, 2) : u_{R_2}(t) = u_{C}(t), u_{R_1}(t)= E - u_{R_2}(t) = E - u_{C}(t)$
\[\Leftrightarrow \dfrac{E - u_{C}(t)}{R_1} - \dfrac{u_{C}(t)}{R_2} = C \dfrac{du_C}{dt}\]Il ne reste plus qu’à remettre l’équation en forme :
\[\Leftrightarrow C \dfrac{du_C}{dt} = \dfrac{E}{R_1} - \dfrac{u_{C}(t)}{R_1} - \dfrac{u_{C}(t)}{R_2}\] \[\Leftrightarrow C \dfrac{du_C}{dt} + \dfrac{u_{C}(t)}{R_1} + \dfrac{u_{C}(t)}{R_2}= \dfrac{E}{R_1}\] \[\Leftrightarrow C \dfrac{du_C}{dt} + R_2\dfrac{u_{C}(t)}{R_1R_2} + R_1\dfrac{u_{C}(t)}{R_1R_2}= \dfrac{E}{R_1}\] \[\Leftrightarrow C \dfrac{du_C}{dt} + \dfrac{R_1+R_2}{R_1R_2}u_C(t)= \dfrac{E}{R_1}\] \[\Leftrightarrow \boxed{\dfrac{du_C}{dt} + \dfrac{R_1+R_2}{R_1R_2C}u_C(t)= \dfrac{E}{R_1C}}\]On peut alors résoudre l’équation différentielle :
- Solution particulière : $\dfrac{du_C}{dt} = 0$
- Solution homogène :
D’après le théorème, on a alors : $\boxed{u_{C,h}(t) = \alpha \exp\left(\dfrac{-(R_1+R_2)t}{R_1R_2C}\right)}$
- Conclusion :
On détermine $\alpha$ grâce à la condition initiale $u_C(t=0)=0$ :
\[u_C(t=0) = 0\] \[\Leftrightarrow \dfrac{ER_2}{R_1+R_2} + \alpha \exp\left(\dfrac{-(R_1+R_2).0}{R_1R_2C}\right) = 0\] \[\Leftrightarrow \dfrac{ER_2}{R_1+R_2} + \alpha .1 = 0\] \[\Leftrightarrow \alpha = - \dfrac{ER_2}{R_1+R_2}\]Et on en déduit finalement :
\[\boxed{u_C(t) = \dfrac{ER_2}{R_1+R_2}\left(1 - \exp\left(\dfrac{-(R_1+R_2).t}{R_1R_2C}\right)\right)}\]Dans ces cas là, il peut être utile de poser $\tau = \dfrac{R_1R_2C}{R_1+R_2}$ afin de simplifier l’écriture de l’équation :
\[\boxed{u_C(t) = \dfrac{ER_2}{R_1+R_2}\left(1 - \exp\left(\dfrac{-t}{\tau}\right)\right)}\]- Lorsqu’on rouvre l’interrupteur :
- Le circuit redevient un simple circuit RC série
- La condition initiale devient le régime permanent de l’étude précédente, donc $u_C(t=0) = \frac{ER_2}{R_1+R_2}$
L’équation différentielle est alors la même que celle du cours :
$\boxed{\dfrac{du_C}{dt} +\dfrac{u_C(t)}{R_1C} = \dfrac{E}{R_1C}}$
Résolution :
- Solution particulière :
\(\dfrac{1}{R_1C} u_{C,p}(t) = \dfrac{E}{R_1C}\) \(\Leftrightarrow \boxed {u_{C,p}(t) = E}\)
- Solution homogène :
- Conclusion (et détermination de la constante $\alpha$) :
La solution complète de l’équation différentielle est :
\[u_C(t) = u_{C,p}(t) + u_{C,h}(t) = E + \alpha e^{-\frac{t}{R_1C}}\]Or, \(u_C(t=0) = \dfrac{ER_2}{R_1+R_2}\) \(\Leftrightarrow E + \alpha e^{-\frac{0}{R_1C}} = \dfrac{ER_2}{R_1+R_2}\) \(\Leftrightarrow \alpha = \dfrac{ER_2}{R_1+R_2} - E\) \(\Leftrightarrow \alpha = \dfrac{ER_2}{R_1+R_2} - E\dfrac{R_1 + R_2}{R_1+R_2}\) \(\Leftrightarrow \alpha = -\dfrac{ER_1}{R_1+R_2}\)
Et on peut donc finalement écrire que :
\[\boxed{u_{C}(t) = E -\dfrac{ER_1}{R_1+R_2}e^{-\frac{t}{R_1C}}}\]3. Bobine
Une bobine, parfois nommée inductance, est un enroulement de fil conducteur (on appellera communément un tour de fil : une spire). Dans le cours de deuxième année, nous verrons comment la bobine est un élément central pour créer des champs magnétiques, ce qui en fait un élément prépondérant dans de nombreux systèmes usuels (transformateurs, chargeurs à induction, systèmes de freinage magnétique […])
Pour la partie qui nous intéresse aujourd’hui, une bobine présente tout comme le condensateur un comportement transitoire dans un circuit électrique.
Lorsqu’un condensateur est soumis à un échelon de tension, la réponse n’est pas immédiate, le condensateur freine l’établissement de la tension dans le circuit. Nous allons voir que pour la bobine, il en va de même pour létablissement du courant dans le circuit.
A. Les maths
Pour un condensateur, le retard induit sur la tension se traduisait par l’équation : $i_C(t) = C \dfrac{du_C}{dt}$.
Pour la bobine, on va écrire la relation ‘symétrique’, en remplaçant l’intensité par la tension et vice versa.
On a donc comme relation caractéristique pour la bobine : $u_L(t) = L \dfrac{di_L}{dt}$.
$L$ est la propriété caractéristique de la bobine, nommée l’inductance (la lettre L provient du physicien prussien Lenz). $L$ s’exprime en henry ($H$), et sera typiquement de l’ordre du $mH$ dans les circuits que nous étudierons.
Remarque : On verra par la suite que la grande majorité des raisonnements que nous avons effectués dans le cadre de l’étude du condensateur seront valables, en remplaçant la tension du condensateur par l’intensité dans la bobine.
B. Circuit RL série : établissement du courant
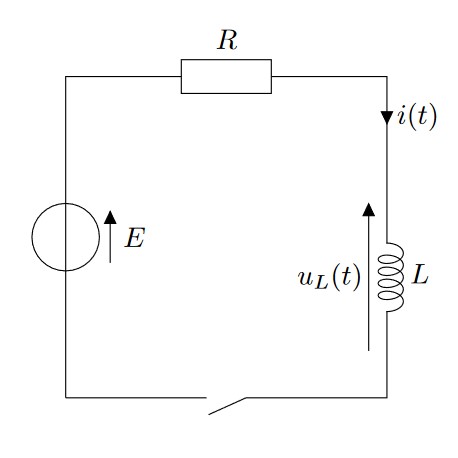
On va étudier l’établissement dans un circuit RL série dans la situation représentée sur le schéma précédent.
- A $t=0$, on ferme l’interrupteur.
- Cela veut dire qu’à $t<0$, $i = 0$ dans le circuit.
Équations caractéristiques du circuit
- Loi des mailles : $(1) : E = u_R(t) + u_L(t)$
- Loi d’Ohm : $(2) : u_R(t) = R.i(t)$
- Loi de la bobine : $(3) : u_L(t) = L \dfrac{di}{dt}$
On va maintenant combiner ces trois équations afin d’obtenir une équation unique qui ne contient que $i(t)$.
Remarque : On va ici résoudre pour $i(t)$ et non pas $u_L(t)$. Nous justifierons ce choix à la fin de l’exemple.
Équation différentielle en $i(t)$
$(3) : u_L(t) = L \dfrac{di}{dt}$
On élimine $u_L(t)$ en utilisant $(1) : u_L(t) = E - u_R(t)$
$\Leftrightarrow E - u_R(t) = L \dfrac{di}{dt}$
On élimine $u_R(t)$ en utilisant $(2) : u_R(t) = R.i(t)$
$\Leftrightarrow E - R.i(t)= L \dfrac{di}{dt}$
Il ne reste qu’à remettre en forme l’équation :
$\Leftrightarrow L \dfrac{di}{dt} + R.i(t) = E$
$\Leftrightarrow \boxed{\dfrac{di}{dt} + \dfrac{R}{L}i(t) = \dfrac{E}{L}}$
Il s’agit d’une équation qu’on peut comparer à celle obtenue pour la tension aux bornes du condensateur lors de la charge.
Résolution de l’équation différentielle
- Solution particulière $i_{p}(t)$:
On cherche la solution en régime permanent : $\frac{di}{dt} = 0$. L’équation devient alors : \(\dfrac{R}{L} i_{p}(t) = \dfrac{E}{L}\) \(\Leftrightarrow \boxed {i_{p}(t) = \dfrac{E}{R}}\)
- Solution homogène $i_{h}(t)$:
On écrit l’équation dite “sans second membre” : \(\dfrac{di_{h}}{dt} + \dfrac{R}{L} i_{h}(t) = 0\)
Théorème : L’équation $y’(t) + a.y(t) = 0$ a pour solution : $y(t) = \alpha e^{-at}$ où $\alpha$ est une constante à déterminer.
Donc ici, on peut en déduire que $\boxed{i_{h}(t) = \alpha e^{-\frac{Rt}{L}}}$
- Conclusion (et détermination de la constante $\alpha$) :
La solution complète de l’équation différentielle est :
\[i(t) = i_{p}(t) + i_{h}(t) = \dfrac{E}{R} + \alpha e^{-\frac{Rt}{L}}\]Ici, on sait que $i(t=0) = 0$.
Alors, \(i(t=0) = 0\) \(\Leftrightarrow \dfrac{E}{R} + \alpha e^{-\frac{R.0}{L}} = 0\) \(\Leftrightarrow \dfrac{E}{R} + \alpha \times 1 = 0\) \(\Leftrightarrow \alpha = -\dfrac{E}{R}\)
Et on peut donc finalement écrire que : \(i(t) = \dfrac{E}{R} - \dfrac{E}{R} e^{-\frac{Rt}{L}}\)
ou encore :
\[\boxed{i(t) = \dfrac{E}{R}\left(1 - e^{-\frac{Rt}{L}}\right)}\]Le tracé de la courbe sera le même que pour la tension dans un condensateur ! (Peu de surprises, c’était la même équation différentielle)
Remarque importante :
Lorsqu’on calcule la tension aux bornes de la bobine, on obtient :
\[u_L(t) = L \dfrac{di}{dt} = E e^{-\frac{Rt}{L}}\]La tension aux bornes de la bobine est nulle à $t<0$. Or, d’après la formule ci-dessus, $u_L(t = 0^+) = E$. Il y a donc une discontinuité de l’intensité dans la bobine au moment ou la charge débute !
C. Suite ?
On pourrait considérer la partie “décharge” de la bobine de la même manière, mais les résultats seront strictement identiques à ceux obtenus pour la partie précédente.
4. Bilans énergétiques
En physique, il est très courant d’utiliser une approche énergétique pour résoudre un problème. En effet, pour tout système, on a toujours conservation de l’énergie : les sources d’énergie doivent compenser les dépenses.
On peut faire un bilan sur l’énergie d’un système (sur une durée donnée) ou bien sur la puissance (à un insant donnée).
En effet, la puissance et l’énergie sont reliés par la relation suivante :
\[\mathscr{E} = \int \mathscr{P}(t)dt \text{, et }\mathscr{P}(t) = \dfrac{\partial \mathscr{E}}{\partial t}\]$\Rightarrow$ La puissance correspond à un ‘débit’ d’énergie.
Dans les paragraphes suivants, nous allons principalement travailler sur les bilans de puissance, ceux-ci ne nécessitant pas le calcul d’intégrales.
A. Puissance délivrée / reçue par un dipôle
Générateur de tension continue :
(Il s’agit d’un dipôle générateur, les formules suivantes sont valides si la tension est orientée dans le même sens que l’intensité)
$\mathscr{P}(t) = E . i(t)$
Par définition $E$ est constant, donc $\mathscr{P}(t)$ ne varie que si $i(t)$ varie.
$\mathscr{E} = \int \mathscr{P}(t)dt = \int E . i(t) dt = E \int i(t)dt$
Résistance :
(Il s’agit d’un dipôle récepteur, les formules suivantes sont valides si la tension est orientée dans le sens opposé à l’intensité)
$\mathscr{P}(t) = u(t) . i(t)$, or $u(t) = R.i(t)$ $\Leftrightarrow \mathscr{P}(t) = R . (i(t))^2 = \dfrac{(u(t))^2}{R}$
Dans le cas de la résistance, on a juste besoin de connaître la tension ou l’intensité afin de calculer la puissance reçue.
La totalité de la puissance reçue par une résistance est transformée en chaleur : c’est l’effet Joule. Dans un circuit classique, cela correspond à des pertes sèches (sauf si on est en train de griller une tartine de pain sur cette résistance)
$\mathscr{E} = \int \mathscr{P}(t)dt = R \int (i(t))^2dt = \dfrac{1}{R} \int (u(t))^2dt$
Condensateur :
(Il s’agit d’un dipôle récepteur, les formules suivantes sont valides si la tension est orientée dans le sens opposé à l’intensité)
$\mathscr{P}(t) = u(t) . i(t)$, or $i(t) = C\dfrac{du}{dt}$ $\Leftrightarrow \mathscr{P}(t) = u(t) . C\dfrac{du}{dt} =C .u(t) \dfrac{du}{dt}$
$\mathscr{E} = \int \mathscr{P}(t)dt = C \int u(t) \dfrac{du}{dt}dt = \left[ C. \dfrac{(u(t))^2}{2}\right]$ (cf. cours de maths sur l’intégration dans le doute)
On peut remarquer ici que le condensateur ne consomme pas d’énergie. Il la stocke (sous forme de tension) et peut la restituer ensuite en intégralité.
Bobine :
(Il s’agit d’un dipôle récepteur, les formules suivantes sont valides si la tension est orientée dans le sens opposé à l’intensité)
$\mathscr{P}(t) = u(t) . i(t)$, or $u(t) = L\dfrac{di}{dt}$ $\Leftrightarrow \mathscr{P}(t) = L\dfrac{di}{dt} i(t)=L .i(t) \dfrac{di}{dt}$
$\mathscr{E} = \int \mathscr{P}(t)dt = L \int i(t) \dfrac{di}{dt}dt = \left[ L. \dfrac{(i(t))^2}{2}\right]$ (cf. cours de maths sur l’intégration dans le doute)
On peut remarquer ici que la bobine ne consomme pas d’énergie. Elle la stocke (sous forme de courant électrique) et peut la restituer ensuite en intégralité.
Remarque : (cf. TP 3) En pratique, sachant qu’une bobine est constituée d’une grande longueur de fil conducteur, toute bobine est (un peu) résistante. On parle de résistance interne de la bobine. On distinguera donc dans l’étude la bobine idéale ($R=0$) et la bobine réelle ($R\neq 0$)
B. Bilan de puissance du circuit RL série

On va étudier la phase d’établissement du courant :
\[i(t) = \dfrac{E}{R} (1 - e^{-\frac{Rt}{L}})\]Puissance fournie au circuit ?
Dans ce circuit, il y a un unique élément générateur (le générateur..) :
$\mathscr{P}_{in}(t) = E.i(t) = \dfrac{E^2}{R} (1 - e^{-\frac{Rt}{L}})$
A un instant $t$, le générateur fournit la puissance $\mathscr{P}_{in}(t)$ au circuit.
Les lois de la physique étant (généralement) bien faites, on devrait trouver la même chose lorsqu’on calcule $\mathscr{P}_{out}(t)$ !
Puissance reçue par le circuit :
Dans ce circuit, il y a deux éléments récepteurs : la bobine et la résistance.
$\mathscr{P}_{out}(t) = \mathscr{P}_L(t) + \mathscr{P}_R(t)$
$\Leftrightarrow \mathscr{P}_{out}(t) = L.i(t)\dfrac{di}{dt} + R(i(t))^2$
On commence par calculer : $\mathscr{P}_R(t) = R(i(t))^2$ $\Leftrightarrow \mathscr{P}_R(t) = R \left( \dfrac{E}{R} (1 - e^{-\frac{Rt}{L}})\right)^2$ $\Leftrightarrow \mathscr{P}_R(t) = \cancel R \dfrac{E^2}{R^{\cancel 2}} \left( 1 - e^{-\frac{Rt}{L}}\right)^2$ $\Leftrightarrow \mathscr{P}_R(t) = \dfrac{E^2}{R}\left(1 - 2e^{-\frac{Rt}{L}} + e^{-\frac{2Rt}{L}}\right)$
Puis pour la puissance dans la bobine :
$\dfrac{di}{dt} = \dfrac{d}{dt} \left( \dfrac{E}{R} - \dfrac{E}{R}e^{-\frac{Rt}{L}}\right)$ $\Leftrightarrow \dfrac{di}{dt} = \dfrac{d}{dt} \left( \dfrac{E}{R}\right) - \dfrac{d}{dt} \left( \dfrac{E}{R}e^{-\frac{Rt}{L}}\right)$ $\Leftrightarrow \dfrac{di}{dt} = 0 - \dfrac{E}{R}\left(\dfrac{-R}{L}\right)e^{-\frac{Rt}{L}}$ $\Leftrightarrow \dfrac{di}{dt} = \dfrac{E}{L}e^{-\frac{Rt}{L}}$
D’où : $\mathscr{P}_L(t) = L \dfrac{di}{dt}i(t)$ $\Leftrightarrow \mathscr{P}_L(t) = L\left(\dfrac{E}{L}e^{-\frac{Rt}{L}}\right)\dfrac{E}{R}\left(1 - e^{-\frac{Rt}{L}}\right)$ $\Leftrightarrow \mathscr{P}_L(t) = \dfrac{E^2}{R}\left(e^{-\frac{Rt}{L}} - e^{-\frac{2Rt}{L}}\right)$
Donc $\mathscr{P}_{out}(t) =\mathscr{P}_R(t) + \mathscr{P}_L(t)$
$\Leftrightarrow \mathscr{P}_{out}(t) = \dfrac{E^2}{R}\left(1 - 2e^{-\frac{Rt}{L}} + e^{-\frac{2Rt}{L}}\right) + \dfrac{E^2}{R}\left(e^{-\frac{Rt}{L}} - e^{-\frac{2Rt}{L}}\right)$
$\Leftrightarrow \mathscr{P}_{out}(t) = \dfrac{E^2}{R} \left(1 - e^{-\frac{Rt}{L}} \right) = \mathscr{P}_in(t)$
On retrouve bien que la puissance générée est égale à la puissance consommée dans le circuit $\Rightarrow$ On a bien conservation de l’énergie dans le circuit, on est contents !