Chapitre 4 : Régimes Transitoires - EXERCICES
Exercice 1 :
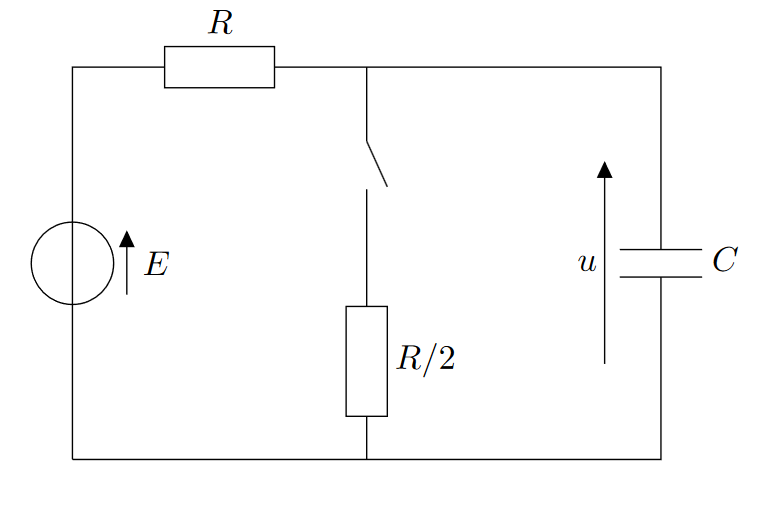
On considère le montage ci-dessus. Initialement, le condensateur est déchargé, le générateur est éteint, et l’interrupteur est ouvert.
- L’interrupteur reste ouvert, et on allume le générateur. Déterminer $u(t)$, et préciser la constante de temps de ce circuit.
- On suppose que le régime permanent de la question précédente est atteint depuis longtemps, et on ferme l’interrupteur. On choisit cet instant comme nouvelle origine des temps. Donner l’équation différentielle alors vérifiée par $u(t)$, et la résoudre.
- Tracer la courbe de l’évolution de $u_C(t)$ sur les deux phases.
- Effectuer un bilan de puissance sur les deux phases.
Exercice 2 :
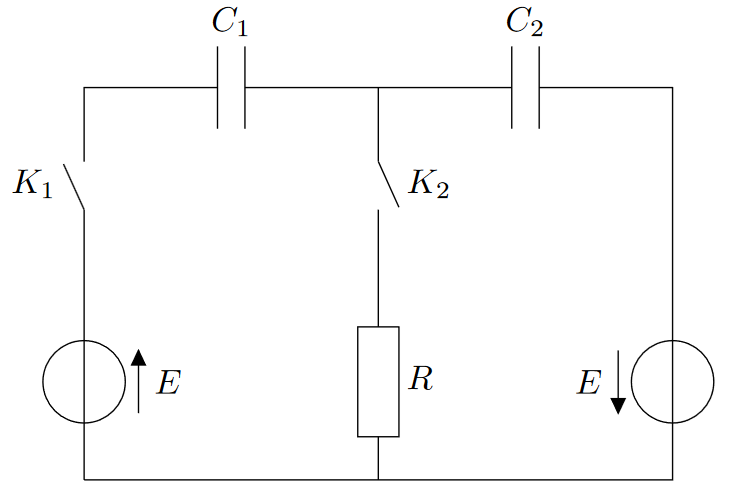
On considère le montage ci-dessus. Initialement, les deux condensateurs sont déchargés, et les interrupteurs $K_1$ et $K_2$ sont ouverts.
- L’interrupteur $K_2$ restant ouvert, on ferme $K_1$ pendant un temps assez long pour les tensions sur les condensateurs $C_1$ et $C_2$ deviennent constantes en fonction du temps. Déterminer les valeurs de ces tensions lorsqu’elles sont devenues constantes.
- On ferme l’interrupteur $K_2$. Déterminer les nouvelles valeurs de la tension dans chacun des condensateurs lorsqu’elles sont devenues constantes. Quel est le temps nécessaire pour que cela se produise ?
Exercice 3 :
On relie à une résistance $R$ deux condensateurs de capacité $C_1$ et $C_2$ initialement chargés. À $t=0$, on ferme l’interrupteur. Pour $t<0$, on a $u_1(t<0) = U_{01}$ et $u_2(t<0) = U_{02}<U_{01}$
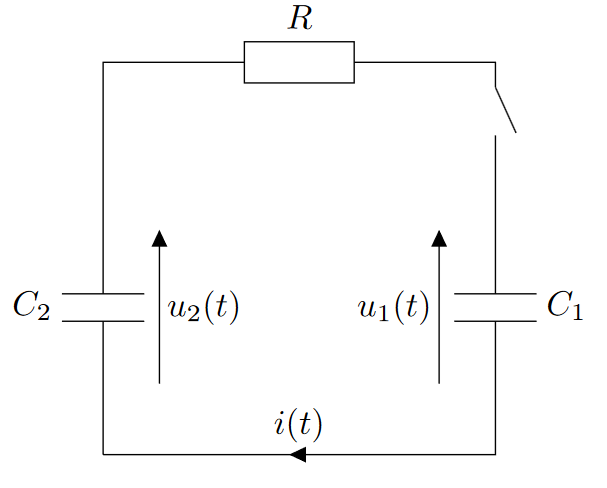
- Déterminer l’équation différentielle vérifiée par le courant $i(t)$ puis la résoudre.
- En déduire $u_1(t)$ et $u_2(t)$.
- Représenter sur un graphique $u_1(t)$, $u_2(t)$, et $u_R(t)$.
- Déterminer $u_1(t\to\infty)$ et $u_2(t\to\infty)$
- Calculer la variation d’énergie stockée dans chaque condensateur et l’énergie dissipée par effet Joule dans la résistance. Commenter.
Données : $C_1 = 1\mu F$, $C_2 = 2\mu F$, $U_{01} = 50 V$, $U_{02} = 30 V$, $R = 1 k \Omega$
Exercice 4 :
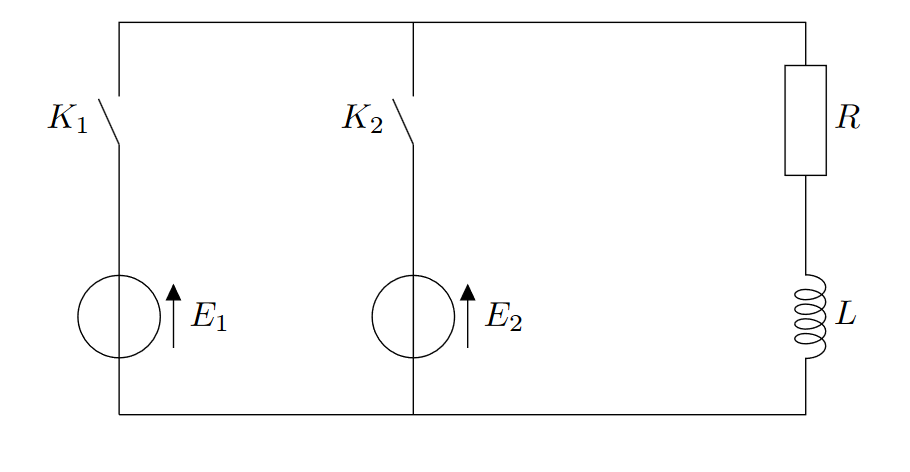
Dans le circuit ci-dessus, les interrupteurs $K_1$ et $K_2$ sont ouverts depuis un très long temps.
À $t=0$, on ferme l’interrupteur $K_1$.
- Calculer l’expression du courant qui circule dans la bobine.
- On considère que le régime permanent est atteint depuis longtemps, puis on ferme $K_2$ en même temps qu’on ouvre $K_1$. On choisit cet instant comme nouvelle origine des temps. Donner l’expression du courant qui circule dans la bobine.
- Que se passe-t-il si on réduit le temps entre les manipulations d’interrupteurs?
Exercice 5 :
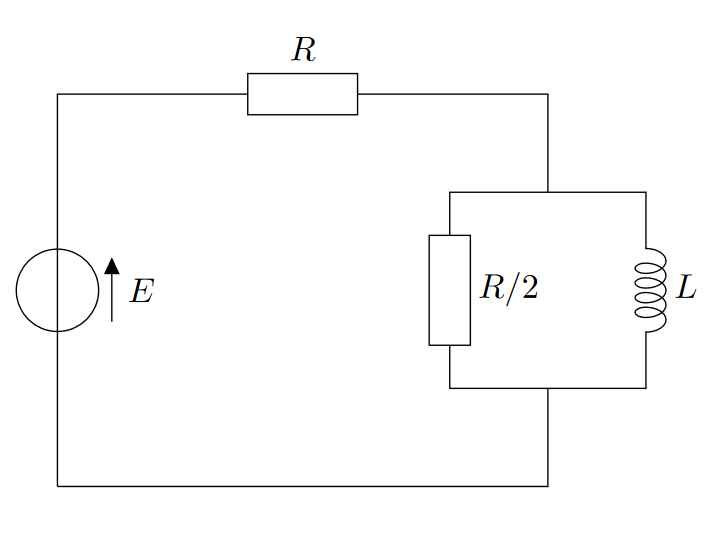
Le circuit ci-dessus est alimenté par un générateur idéal de tension continue, et délivre une tension $E$. À l’instant $t=0$, on allume ce générateur.
- Le courant dans la bobine est-il continu en $t=0$ ? En déduire $i(t=0^+)$
- Déterminer le comportement de $i(t\to\infty)$.
- Établir et résoudre l’équation différentielle vérifiée par le courant circulant dans la bobine.
- Exprimer en fonction de $L$ et $R$ le temps $t_1$ au bout duquel le courant dans la bobine atteint $90\%$ de sa valeur maximale.
- Une fois le régime permanent atteint, on éteint le générateur et on choisit comme nouvelle origine des temps cet instant. Donner la nouvelle expression du courant dans la bobine.
- Réaliser un bilan de puissance sur les deux phases.
Exercice 6 :
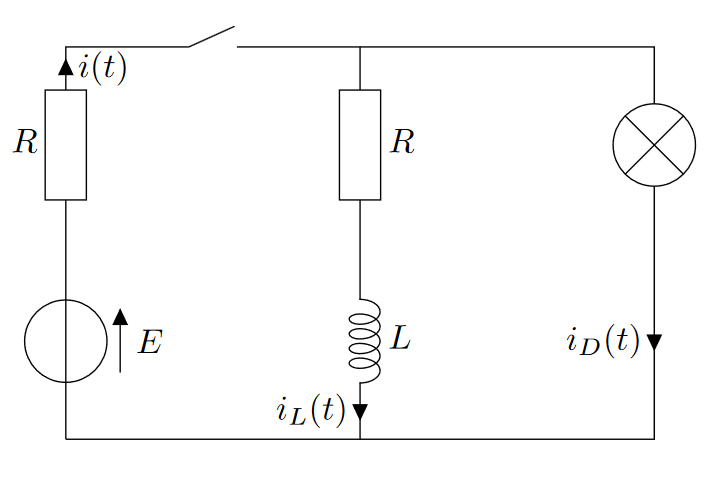
On considère le montage ci-dessus. À $t=0$, on ferme l’interrupteur. La lampe se comporte comme une résistance de valeur $4R$.
- Donner $i_L(0^+)$, et $i_L(t\to\infty)$.
- Établir et résoudre l’équation différentielle vérifiée par $i_L(t)$. En déduire $i_D(t)$.
- La lampe ne s’allume que pour $\lvert i_D\rvert > E/8R$. Quel est son rôle ?