Chapitre 5 : Oscillateurs électriques
1. Étude du problème de base : le circuit LC série
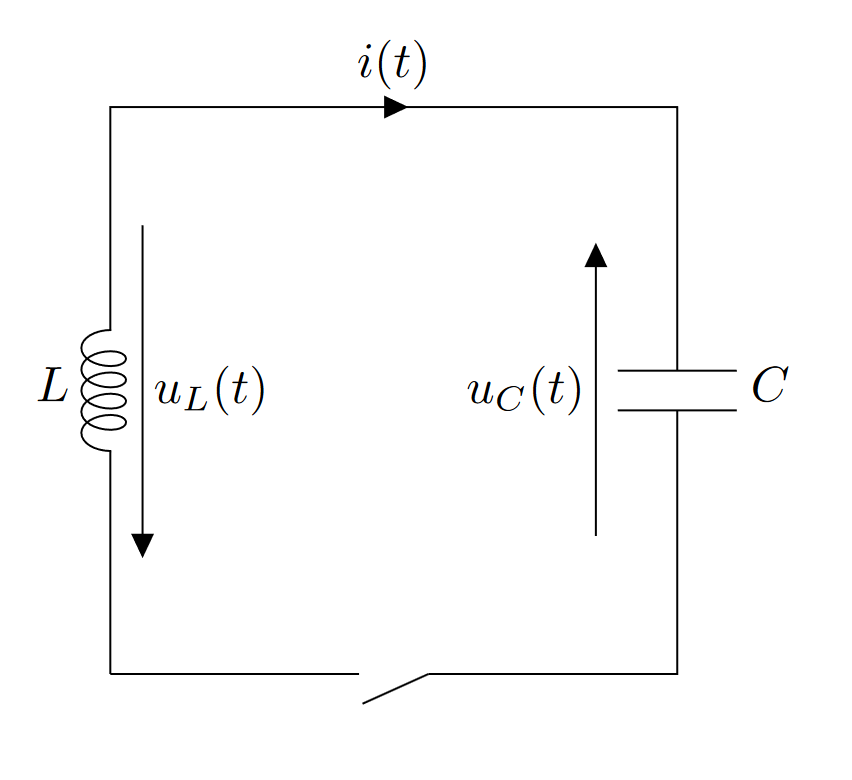
On s’intéresse au circuit représenté ci-dessus. On considère qu’à $t<0$, le condensateur est chargé, et $u_C(t<0) = U_0$.
À $t=0$, on ferme l’interrupteur. On s’intéresse à la tension $u_C(t)$ pour $t>0$.
A. Étude qualitative
On peut se demander comment va évoluer la tension du condensateur. En effet, dans un premier temps, lorsqu’on ferme l’interrupteur, le condensateur va avoir tendance à se décharger. Cependant, la bobine va s’opposer à l’établissement du courant, qui va donc augmenter de manière progressive et non brutale.
Lorsque la tension du condensateur devient nulle, le mouvement de charges devrait alors s’interrompre. Nous savons cependant que l’intensité électrique est continue dans une bobine : la bobine continue à alimenter le mouvement des charges, et va donc forcer la charge du condensateur dans le sens opposé.
Intuitivement, on devrait donc voir apparaître une oscillation de la tension du condensateur entre une valeur positive et une valeur négative.
B. Étude quantitative
On procède de la même manière que dans le chapitre précédent.
Équations caractéristiques du circuit :
- Loi des mailles : $(1) : 0 = u_C(t) + u_L(t)$
- Loi du condensateur : $(2) : i(t) = C \dfrac{du_C}{dt}$
- Loi de la bobine : $(3) : u_L(t) = L \dfrac{di}{dt}$
Établissement de l’équation différentielle en $u_C(t)$ :
On part de l’équation $(2) : i(t) = C \dfrac{du_C}{dt}$.
On voudrait éliminer $i(t)$, mais on ne dispose que de l’équation $(3)$ qui contient $\frac{di}{dt}$ et non pas $i(t)$. Il va donc falloir dériver l’équation $(2)$ pour pouvoir utiliser l’équation $(3)$ !
$(2) \Rightarrow \dfrac{di}{dt} = C \dfrac{d^2u_C}{dt^2}$ où $\dfrac{d^2u_C}{dt^2}$ représente la dérivée seconde de $u_C(t)$.
Et donc en remplaçant grâce à $(3) : \dfrac{di}{dt} = \dfrac{u_L(t)}{L}$
$\Leftrightarrow \dfrac{u_L(t)}{L} = C \dfrac{d^2u_C}{dt^2}$
Et enfin en remplaçant $u_L(t)$ grâce à $(1) : u_L(t) = - u_C(t)$,
$\Leftrightarrow \dfrac{- u_C(t)}{L} = C \dfrac{d^2u_C}{dt^2}$
On remet en forme et on obtient:
$\Leftrightarrow \boxed{\dfrac{d^2u_C}{dt^2} + \dfrac{1}{LC} u_C(t) = 0}$
Que peut-on dire de cette équation ?
- Il s’agit d’une équation différentielle linéaire du second ordre à coefficients réels constants.
- On ne va pas pouvoir appliquer la même méthode de résolution que pour les équations différentielles du premier ordre, car notre théorème pour la solution homogène ne s’applique plus ! Pas de panique, on va en inventer un autre :)
- On remarque que les fonctions qui vérifient cette équation sont les fonctions trigonométriques !
- On appelle ce genre de système un oscillateur harmonique.
C. L’oscillateur harmonique
Un oscillateur harmonique est un oscillateur idéal dont l’évolution au cours du temps est décrite par une fonction sinusoïdale, dont la fréquence ne dépend que des caractéristiques du système et dont l’amplitude est constante. (Wikipédia)
Il faut comprendre dans le mot idéal, un oscillateur sans frottements. Dans ce cas, il n’y a aucune perte d’énergie, et le mouvement peut être entretenu de manière infinie.
On écrit l’équation différentielle caractéristique d’un oscillateur harmonique sous la forme suivante :
\[\boxed{\dfrac{d^2y}{dt^2} + {\omega_0}^2 y(t) = 0}\]Et la solution s’écrit sous la forme :
\[\boxed{y(t)= y_0 \cos (\omega_0 t + \varphi)}\](On verra dans la suite du cours comment retrouver cette solution)
Et on appelle :
- $\omega_0$ la pulsation propre du mouvement
- $y_0$ l’amplitude du mouvement
- $\varphi$ la phase à l’origine des temps
$\omega_0$ est déterminé à partir de l’équation différentielle, tandis que $y_0$ et $\varphi$ sont déterminés à partir des conditions initiales.
On pourra donc retrouver (par exemple) la période des oscillations en utilisant les formules du cours sur les ondes ! $T = \frac{2\pi}{\omega_0}$
2. La réalité : l’oscillateur harmonique amorti
En pratique, il existe souvent une limite physique aux systèmes qu’on approxime à des oscillateurs harmoniques : il existe une dissipation d’énergie.
A. Le circuit RLC série

On s’intéresse donc au circuit représenté ci-dessus. A la différence du circuit LC, la résistance va ici consommer une partie de l’énergie du circuit, réduisant peu à peu l’amplitude des oscillations.
En procédant de la même manière qu’au début du chapitre, on va établir l’équation différentielle, et identifier les termes caractéristiques.
Équations caractéristiques du circuit :
- Loi des mailles : $(1) : 0 = u_C(t) + u_R(t) + u_L(t)$
- Loi du condensateur : $(2) : i(t) = C \dfrac{du_C}{dt}$
- Loi de la bobine : $(3) : u_L(t) = L \dfrac{di}{dt}$
- Loi d’Ohm : $(4) : u_R(t) = R. i(t)$
Établissement de l’équation différentielle en $u_C(t)$ :
On part de l’équation $(2) : i(t) = C \dfrac{du_C}{dt}$.
On voudrait éliminer $i(t)$, mais on ne dispose que de l’équation $(3)$ qui contient $\frac{di}{dt}$ et non pas $i(t)$. Il va donc falloir dériver l’équation $(2)$ pour pouvoir utiliser l’équation $(3)$ !
$(2) \Rightarrow \dfrac{di}{dt} = C \dfrac{d^2u_C}{dt^2}$ où $\dfrac{d^2u_C}{dt^2}$ représente la dérivée seconde de $u_C(t)$.
Et donc en remplaçant grâce à $(3) : \dfrac{di}{dt} = \dfrac{u_L(t)}{L}$
$\Leftrightarrow \dfrac{u_L(t)}{L} = C \dfrac{d^2u_C}{dt^2}$
Et enfin en remplaçant $u_L(t)$ grâce à $(1) : u_L(t) = -u_R(t) - u_C(t)$,
$\Leftrightarrow \dfrac{ -u_R(t)- u_C(t)}{L} = C \dfrac{d^2u_C}{dt^2}$
Ici, on doit utiliser $(4)$ pour remplacer $u_R(t) = R .i(t)$, puis avec $(2) : u_R(t) = RC\dfrac{du_C}{dt}$
$\Leftrightarrow -\dfrac{1}{L}RC\dfrac{du_C}{dt} - \dfrac{u_C(t)}{L} = C \dfrac{d^2u_C}{dt^2}$
On remet en forme et on obtient:
$\Leftrightarrow \boxed{\dfrac{d^2u_C}{dt^2} + \dfrac{R}{L}\dfrac{du_C}{dt} + \dfrac{1}{LC} u_C(t) = 0}$
Que peut-on dire de cette équation ?
-
Il s’agit d’une équation différentielle linéaire du second ordre à coefficients réels constants.
-
Cette fois-ci, on a un terme d’ordre 1, on ne vas pas pouvoir résoudre avec une fonction trigonométrique.
-
On appelle ce genre de système un oscillateur harmonique amorti.
B. L’oscillateur harmonique amorti
Dans ce cas, on considère tout simplement un oscillateur harmonique, mais en prenant en compte la dissipation de l’énergie. Il existera alors un temps caractéristique de dissipation.
On écrit l’équation différentielle caractéristique d’un oscillateur harmonique amorti sous la forme suivante :
\[\boxed{\dfrac{d^2y}{dt^2} + \dfrac{2}{\tau} \dfrac{dy}{dt} + {\omega_0}^2 y(t) = 0}\]On retrouve la même équation que pour l’oscillateur harmonique, avec le terme de premier ordre qui correspondra au terme d’amortissement.
Il existe plusieurs façons d’écrire la solution de cette équation, qui dépendent de la relation entre $\tau$ et $\omega_0$.
Cette fois-ci, pas le choix…
C. Les maths
On reprend l’équation :
\[\boxed{\dfrac{d^2y}{dt^2} + \dfrac{2}{\tau} \dfrac{dy}{dt} + {\omega_0}^2 y(t) = 0}\]On va chercher les fonctions exponentielles qui vérifient cette équation. Pour ce faire, on suppose que $y(t) = \alpha e^{at}$.
Alors on a : $\dfrac{dy}{dt} = a \alpha e^{at} = a y(t)$, et $\dfrac{d^2y}{dt^2} = a^2 \alpha e^{at} = a^2 y(t)$.
On peut réinjecter dans l’équation initiale et on obtient :
\[\Leftrightarrow a^2 y(t) + \dfrac{2}{\tau} .(a y(t)) + {\omega_0}^2 y(t) = 0\]On peut simplifier partout par $y(t)$ pour obtenir :
\[\boxed{a^2 + \dfrac{2}{\tau}a + {\omega_0}^2 = 0}\]Le coefficient $a$ vérifie donc une équation d’ordre 2, c’est ce qu’on appelle le polynôme caractéristique de l’équation différentielle.
On va distinguer les trois cas de l’équation de degré 2 en fonction du signe de $\Delta$.
On a $\Delta = \frac{4}{\tau^2} - 4{\omega_0}^2 = 4(\frac{1}{\tau^2}-{\omega_0}^2)$
$\Delta > 0$, les racines sont réelles :
Dans ces cas là, on a deux solutions réelles. La solution pourra s’écrire sous la forme :
\[\boxed{y(t) = A \exp(r_1t) + B \exp(r_2t)}\]où $r_1$ et $r_2$ sont les deux racines du polynôme caractéristique.
\[r_{1,2} = -\frac{1}{\tau} \pm \sqrt{\frac{1}{\tau^2}-{\omega_0}^2}\](En général pour un problème physique, on aura deux racines négatives pour un problème amorti. Sinon la solution tend vers l’infini…Ainsi, on a bien des exponentielles décroissantes, comme pour la charge/décharge d’un condensateur.)
$A$ et $B$ sont déterminés par les conditions initiales du problème.
On appelle cela le régime apériodique. Le système revient vers un état de repos sans oscillations.
$\Delta = 0$, cas limite :
Dans ce cas, la solution s’écrit :
\[\boxed{y(t) = (At + B) \exp(-t/\tau)}\]$A$ et $B$ sont déterminés par les conditions initiales du problème.
Il s’agit du cas limite pour lequel il n’y a pas d’oscillations.
$\Delta < 0$, les racines sont complexes :
Dans ce cas, $r_{1,2} = -\dfrac{1}{\tau} \pm j\sqrt{ {\omega_0}^2-\dfrac{1}{\tau^2}}$
Remarque : En physique, et tout particulièrement en électronique, on a tendance à écrire le nombre complexe $j$ qui correspond à $j^2 = -1$. Le but est de ne pas le confondre avec l’intensité électrique, par exemple.
Afin de simplifier l’écriture de $r_{1,2}$, on va souvent poser : $\omega = \sqrt{ {\omega_0}^2-\dfrac{1}{\tau^2}}$ pour écrire finalement : $r_{1,2} = -\dfrac{1}{\tau} \pm j\omega$
Ce qui permettra d’écrire la solution :
\[\boxed{y(t) = A e^{-\frac{t}{\tau}} \cos(\omega t + \varphi)}\]On appelle ce régime un régime pseudo-périodique. Le système va revenir vers son état de repos en oscillant autour de la position d’équilibre. Ces oscillations sont caractérisées par la pseudo-période $\omega$.
Les trois solutions présentées dans ce paragraphe constituent la solution homogène de l’équation différentielle. Dans l’exemple, cela est suffisant car le second membre est égal à $0$. En revanche, dans certains exercices, il faudra bien effectuer les trois étapes de résolution comme pour les équations différentielles d’ordre 1 dans le chapitre précédent :
- Solution homogène
- Solution particulière
- Conclusion (somme des deux précédents + détermination des constantes à l’aide des conditions initiales)
D. Application à l’étude du circuit RLC série : résolution
On va étudier le circuit pour 3 ensembles de valeurs différentes :
| Valeur | Cas n°1 | Cas n°2 | Cas n°3 |
|---|---|---|---|
| $E$ | $10V$ | $10V$ | $10V$ |
| $R$ | $1 k\Omega$ | $0.1 k\Omega$ | $2 k\Omega$ |
| $L$ | $10mH$ | $1mH$ | $1mH$ |
| $C$ | $1 \mu F$ | $1 nF$ | $1 nF$ |
Cas n°1 :
On commence par calculer les valeurs de $\tau$ et $\omega_0$ :
$\tau = \dfrac{2L}{R} = \dfrac{2\times10.10^{-3}}{10^3} = 20 \mu s$ $\omega_0 = \dfrac{1}{\sqrt{LC}}=\dfrac{1}{\sqrt{10.10^{-3}\times10^{-6}}} = 10^4 rad.s^{-1}$ On peut également calculer $T_0 = \dfrac{2\pi}{\omega_0} \simeq 630 \mu s$, afin de remarquer que $\tau « T_0$.
a. Solution homogène :
On réecrit le polynôme caractéristique : $a^2 + \dfrac{2}{\tau} a + {\omega_0}^2 = 0$, donc $\Delta = \frac{4}{\tau^2} - 4{\omega_0}^2 = 4(\frac{1}{\tau^2}-{\omega_0}^2) = 9,6.10^9 > 0$
On va donc se situer dans le cas du régime apériodique, c’est à dire un amortissement sans oscillations. La solution homogène pour la tension dans le condensateur s’exprime :
\[u_{C,h}(t) = A \exp(r_1t) + B \exp(r_2t)\]avec $r_1 = -\dfrac{1}{\tau} -\sqrt{\dfrac{1}{\tau^2} - {\omega_0}^2} \simeq -1 000 s^{-1}$
et $r_2 = -\dfrac{1}{\tau} +\sqrt{\dfrac{1}{\tau^2} - {\omega_0}^2} \simeq -99 000 s^{-1}$
b. Solution particulière
On peut réécrire l’équation différentielle :
\[\dfrac{d^2u_C}{dt^2} + \dfrac{2}{\tau} \dfrac{du_C}{dt} + {\omega_0}^2 u_C(t) = 0\]Lorsque les dérivées s’annulent, on obtient : $u_{C,p}(t) = 0$
c. Conclusion
On a donc $u_C(t) = u_{C,h}(t) + u_{C,p}(t) = A \exp(r_1t) + B \exp(r_2t)$
Il nous reste à déterminer les constantes $A$ et $B$ grâce aux conditions initiales :
- $u_C(t<0) = U_0$, le condensateur est chargé au début de l’expérience
- $i(t<0) = 0$, l’interrupteur est ouvert au début de l’expérience
On peut alors justifier que:
- $u_C(t=0^+) = U_0$ car la tension est continue dans un condensateur
- $i(t=0^+) = 0$ car l’intensité est continue dans une bobine. De plus, $i(t) = C\frac{du_C}{dt}$ dans un condensateur, donc $\frac{du_C}{dt} (t=0^+) = 0$
On applique cela à la fonction $u_C(t)$ trouvée plus haut (on calcule tout d’abord $\frac{du_C}{dt}$) :
$\dfrac{du_C}{dt} = Ar_1\exp(r_1 t) + Br_2\exp(r_2 t)$
$ $\left{\begin{array}{l} u_C(t=0^+) = U_0 \Leftrightarrow A+B=U_0 \ \dfrac{du_C}{dt}(t=0^+) = 0 \Leftrightarrow A r_1+Br_2=0 \end{array} \right.$$
Il s’agit d’un système de deux équations à deux inconnues à résoudre, on peut par exemple procéder en faisant une combinaison linéaire de lignes : $L_2-r_2\times L_1$ :
$Ar_1 - r_2A = 0 - r_2 U_0$
$\Leftrightarrow A(r_1-r_2) = - r_2 U_0$
$\Leftrightarrow A = \dfrac{r_2}{r_2-r_1} U_0$
et on peut utiliser $A+B$ pour en déduire $B = \dfrac{-r_1}{r_2-r_1} U_0$
Cas n°2 :
$\tau = \dfrac{2L}{R} = \dfrac{2\times1.10^{-3}}{0,1.10^3} = 20 \mu s$ $\omega_0 = \dfrac{1}{\sqrt{LC}}=\dfrac{1}{\sqrt{10^{-3}\times10^{-9}}} = 10^6 rad.s^{-1}$
On peut également calculer $T_0 = \dfrac{2\pi}{\omega_0} \simeq 6.3 \mu s$, afin de remarquer que $\tau « T_0$.
a. Solution homogène :
On réecrit le polynôme caractéristique : $a^2 + \dfrac{2}{\tau} a + {\omega_0}^2 = 0$, donc $\Delta = \frac{4}{\tau^2} - 4{\omega_0}^2 = 4(\frac{1}{\tau^2}-{\omega_0}^2) = -4\times 10^{12} <0$
On va donc se situer dans le cas du régime pseudo-périodique, c’est à dire un amortissement avec oscillations. La solution homogène pour la tension dans le condensateur s’exprime :
\[u_{C,h}(t) = \alpha \exp(\frac{-t}{\tau}) \cos(\omega t + \varphi)\]avec $\omega = \sqrt{ {\omega_0}^2-\dfrac{1}{\tau^2}} \simeq 10^6 rad.s^{-1}$
b. Solution particulière
On peut réécrire l’équation différentielle :
\[\dfrac{d^2u_C}{dt^2} + \dfrac{2}{\tau} \dfrac{du_C}{dt} + {\omega_0}^2 u_C(t) = 0\]Lorsque les dérivées s’annulent, on obtient : $u_{C,p}(t) = 0$
c. Conclusion
On a donc $u_C(t) = u_{C,h}(t) + u_{C,p}(t) = \alpha \exp(\frac{-t}{\tau}) \cos(\omega t + \varphi)$
Il nous reste à déterminer les constantes $\alpha$ et $\varphi$ grâce aux conditions initiales :
- $u_C(0^+) = U_0$
- $\dfrac{du_C}{dt}(0^+) = 0$
(mêmes justifications que dans le cas précédent)
On applique cela à la fonction $u_C(t)$ trouvée plus haut (on calcule tout d’abord $\frac{du_C}{dt}$) :
$\dfrac{du_C}{dt} = -\dfrac{\alpha}{\tau}\exp(\frac{-t}{\tau})\cos(\omega t +\varphi)- \alpha \omega \exp(\frac{-t}{\tau})\sin(\omega t +\varphi)$
\[\left\{\begin{array}{l} u_C(t=0^+) = U_0 \Leftrightarrow \alpha \cos\varphi=U_0 \\ \dfrac{du_C}{dt}(t=0^+) = 0 \Leftrightarrow -\dfrac{\alpha}{\tau}\cos(\varphi)- \alpha \omega \sin(\varphi)=0 \end{array} \right.\]Il s’agit d’un système de deux équations à deux inconnues à résoudre. Dans la deuxième équation, on peut simplifier par $\alpha$ afin d’obtenir une équation avec uniquement $\varphi$ :
$-\dfrac{1}{\tau}\cos(\varphi)- \omega \sin(\varphi)=0$
$\Leftrightarrow -\dfrac{1}{\tau}\cos(\varphi) = \omega \sin(\varphi)$
$\Leftrightarrow \dfrac{-1}{\tau \omega} = \tan(\varphi)$
d’où : $\varphi = \arctan(\dfrac{-1}{\tau \omega})$
Et on pourra utiliser la première équation pour en déduire : $\alpha = \dfrac{U_0}{\cos \varphi}$