Chapitre 5 : Oscillateurs Électriques - EXERCICES
Exercice 1 : Deux bobines en série
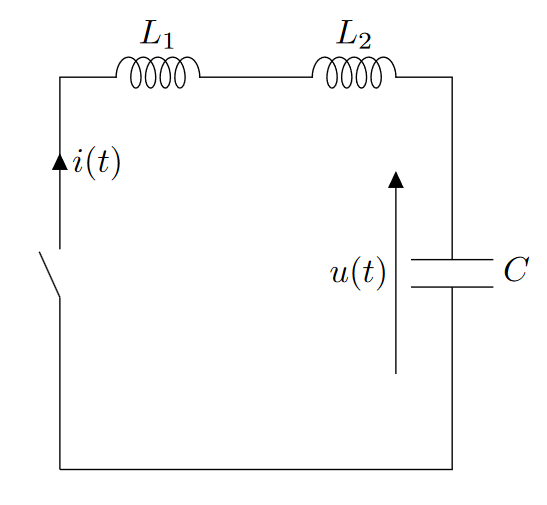
Le circuit schématisé ci-dessus comporte deux bobines d’inductance $L_1$ et $L_2$, ainsi qu’un condensateur de capacité $C$. Le condensateur est initialement chargé, et $u(t<0) = U_0$. À $t=0$, on ferme l’interrupteur.
- Justifier que $u(t=0^+) = U_0$.
- Montrer que $\dfrac{du}{dt}(t=0^+) = 0$
- Déterminer l’équation différentielle vérifiée par $u(t)$.
- Résoudre, qualifier le régime suivi par $u(t)$, et préciser ses caractéristiques. Tracer l’allure de $u(t)$.
Exercice 2 : RLC série
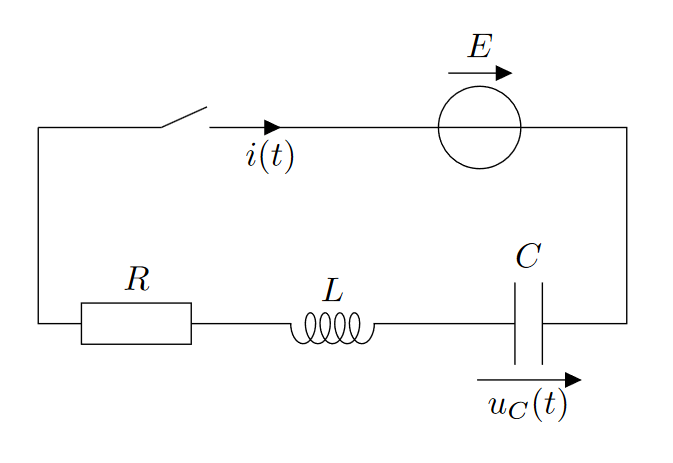
On s’intéresse à l’évolution de la tension $u_C(t)$ aux bornes du condensateur dans le circuit ci-dessus. Avant la fermeture de l’interrupteur à $t=O$, on suppose que le condensateur est déchargé.
- Que vaut la tension $u_C(t)$ en régime permanent (après avoir fermé l’interrupteur) ?
- Établir l’équation différentielle vérifiée par $u_C(t)$. Donner l’expression des grandeurs caractéristiques de cette équation (pulsation propre et facteur d’amortissement, ou facteur de qualité).
- Que valent les conditions initiales $u_C(t=0)$ et $\dfrac{du_C}{dt}(t=0)$ ?
- On prend pour valeurs numériques : $E=10V, R = 1k\Omega, L = 10mH, C = 1\mu F$ a. Qualifier le régime transitoire dans ce cas. b. Résoudre l’équation différentielle pour $u_C(t)$. c. Tracer $u_C(t)$.
- Mêmes questions avec : $E=10V, R = 0.1k\Omega, L = 1mH, C = 1 nF$
- Mêmes questions avec : $E=10V, R = 2k\Omega, L = 1mH, C = 1 nF$
Exercice 3 : Double RC
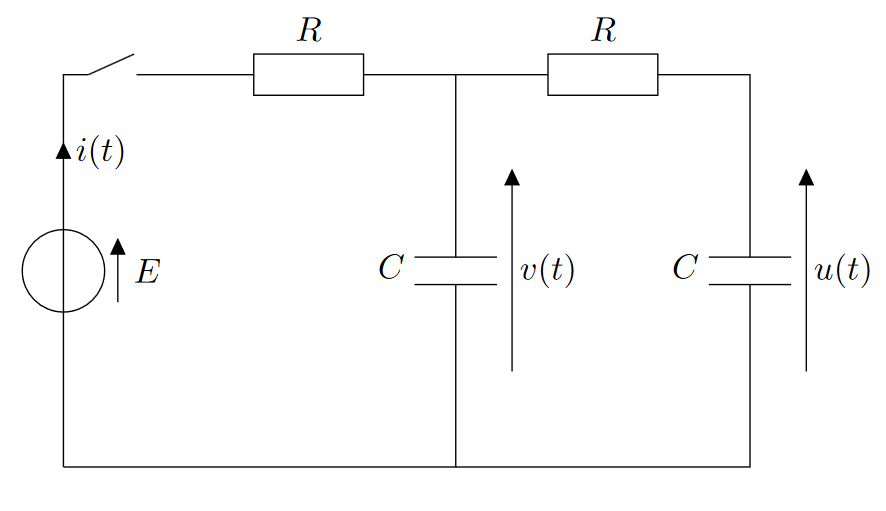
Le circuit ci-dessus comporte deux résistances $R$ identiques, et deux condensateurs de capacité $C$ identiques, et initialement déchargés. À $t=0$, on ferme l’interrupteur.
- Justifier que $u(t=0^+) = 0$.
- Montrer que $\dfrac{du}{dt}(t=0^+) = 0$
- Que vaut la tension $u(t)$ en régime permanent ?
-
Montrer que l’équation différentielle vérifiée par $u(t)$ est : \(\dfrac{E}{\tau^2} = \dfrac{d^2u}{dt^2} + \dfrac{3}{\tau} \dfrac{du}{dt} + \dfrac{u(t)}{\tau^2}\) et donner l’expression de $\tau$.
- Résoudre, qualifier le régime suivi par $u(t)$, et préciser ses caractéristiques. Tracer l’allure de $u(t)$.
Exercice 4 : RL-RC
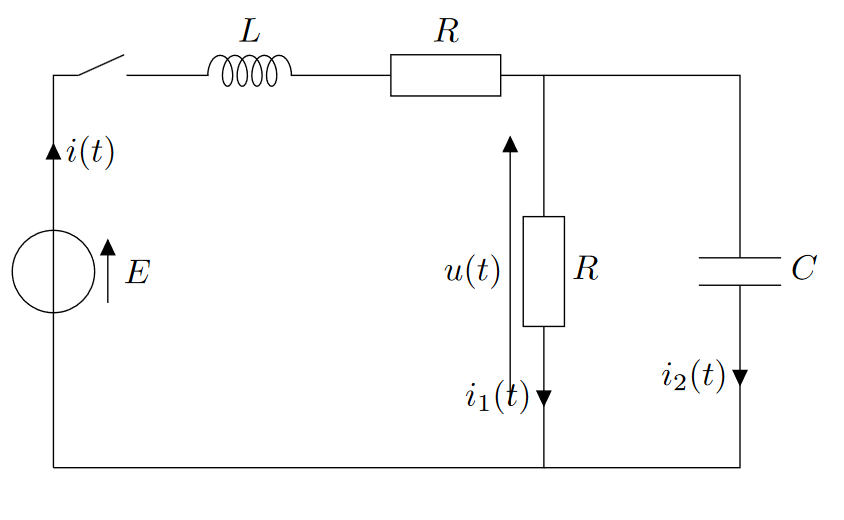
Dans le circuit ci-dessus, les dipôles $RL$ et $RC$ ont la même constante de temps, et $E = 10V$. Pour $t<0$, le condensateur est déchargé. On ferme l’interrupteur à $t=0$.
Déterminer l’équation différentielle vérifiée par $u(t)$. Qualifier le régime de $u(t)$, puis résoudre.
Exercice 5 : RLC parallèle
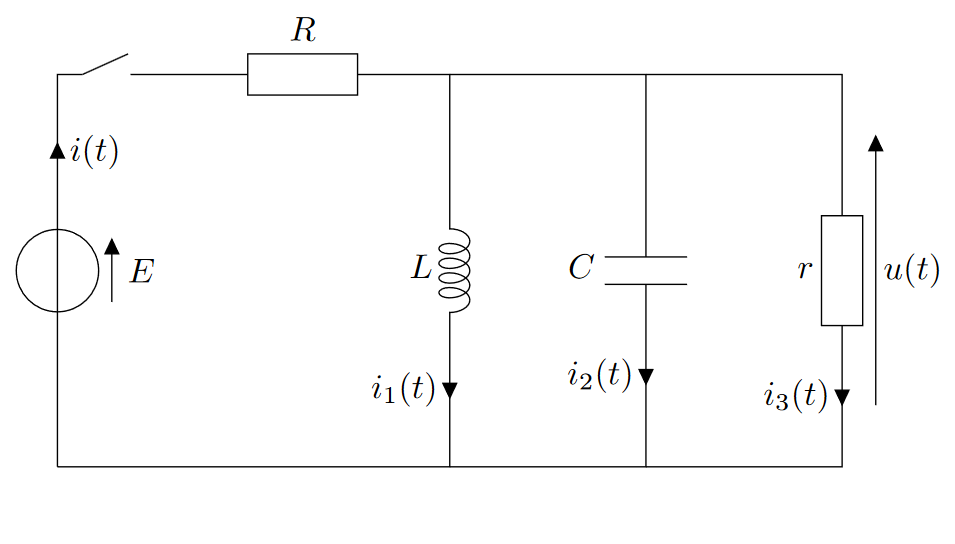
Dans le circuit ci-dessus, on ferme l’interrupteur à $t=0$. On considère qu’avant cela, le condensateur est déchargé. On s’intéresse à l’évolution de la tension $u(t)$.
- Déterminer les valeurs de $u,i,i_1,i_2,i_3$ à $t=0^+$, puis en régime permanent.
- Établir l’équation différentielle vérifiée par $u(t)$. Identifier les grandeurs caractéristiques et donner leur expression.
- Donner la relation entre $R, r, L, C$ pour que le régime soit pseudo-périodique, et exprimer $u(t)$ dans ce cas.