Chapitre 6 : Régime Sinusoïdal Forcé - EXERCICES

Exercice 1 : Impédances équivalentes

Pour chacun des dipôles suivants, déterminer l’impédance complexe équivalente :

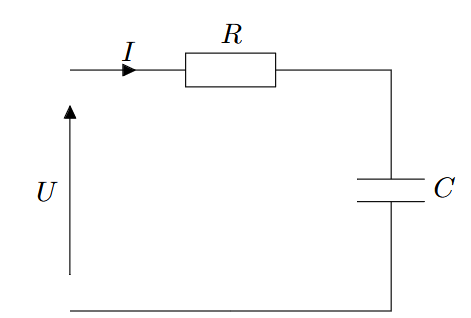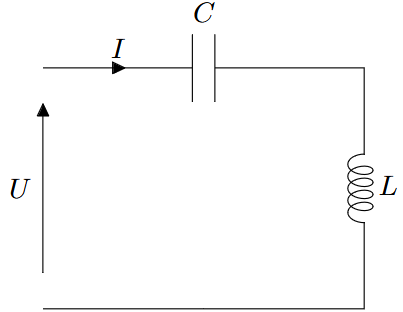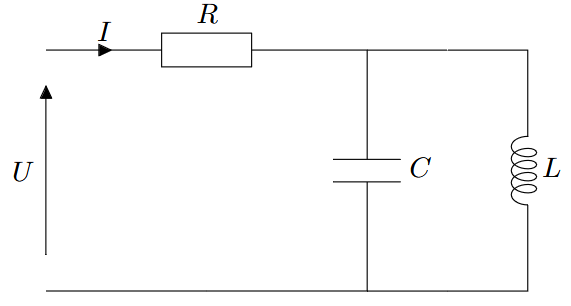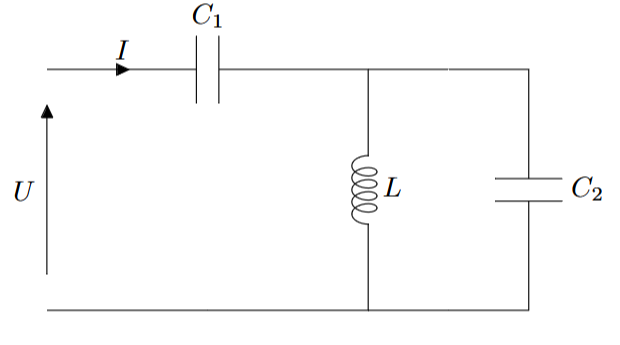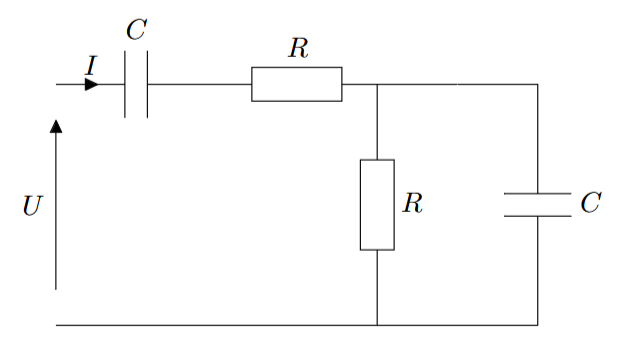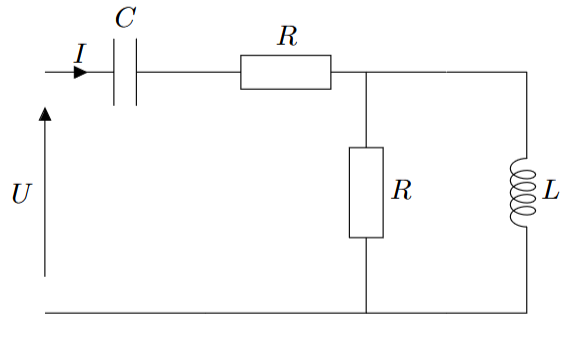Exercice 2 : Détermination d’une équation différentielle à partir des impédances complexes

En reprenant les circuits du TD précédent ci-dessous, déterminer l’équation différentielle recherchée en utilisant les impédances complexes :

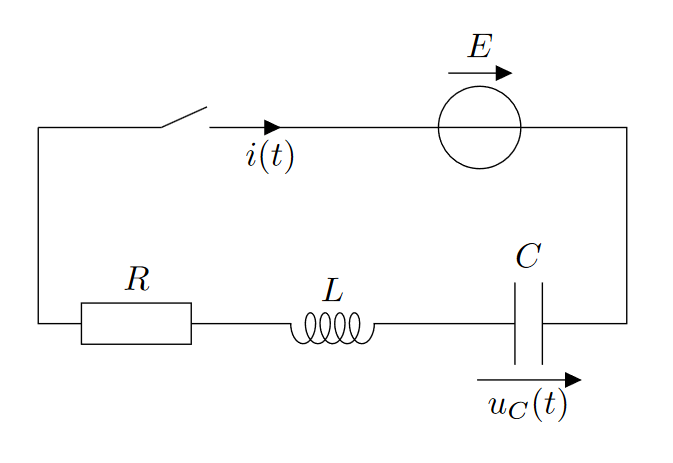
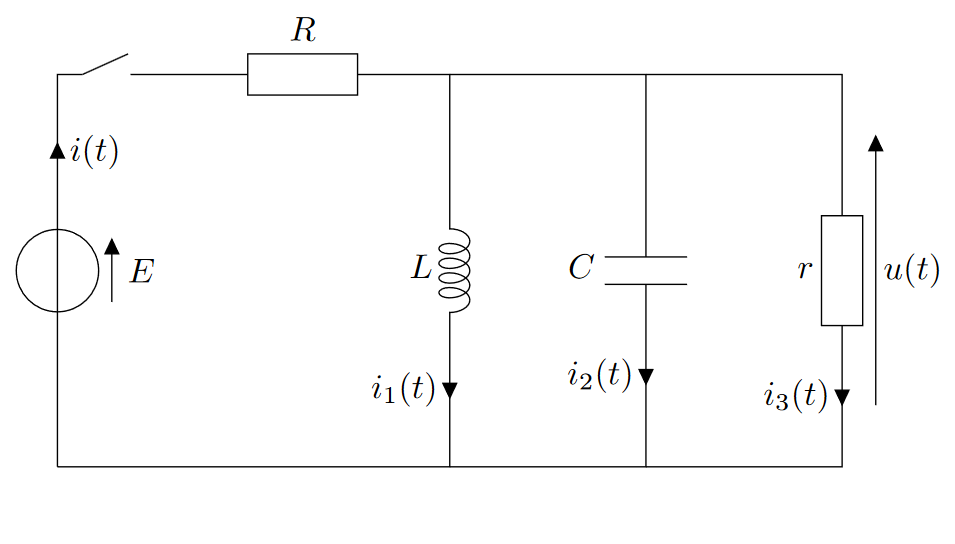
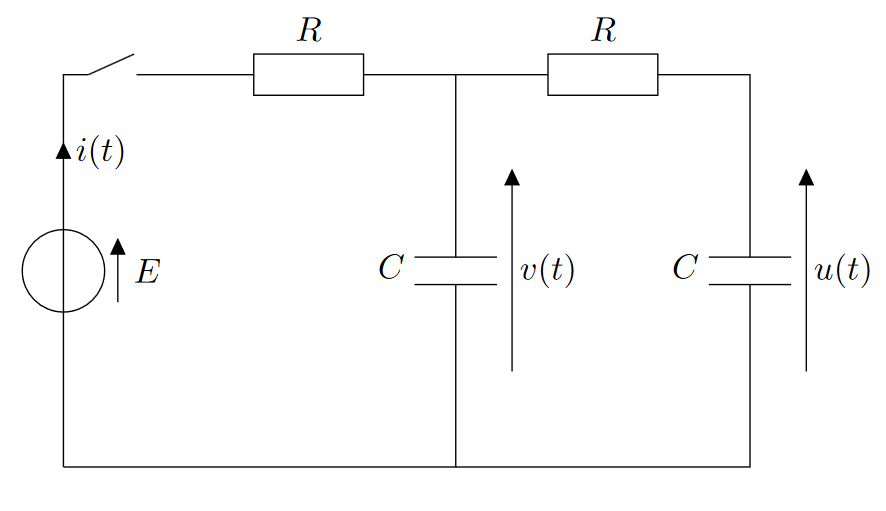
Exercice 3 : Intensités

Un générateur de tension produit la tension : $e = E_0 cos(\omega t)$.

Déterminer les intensités $i_1$ et $i_2$.

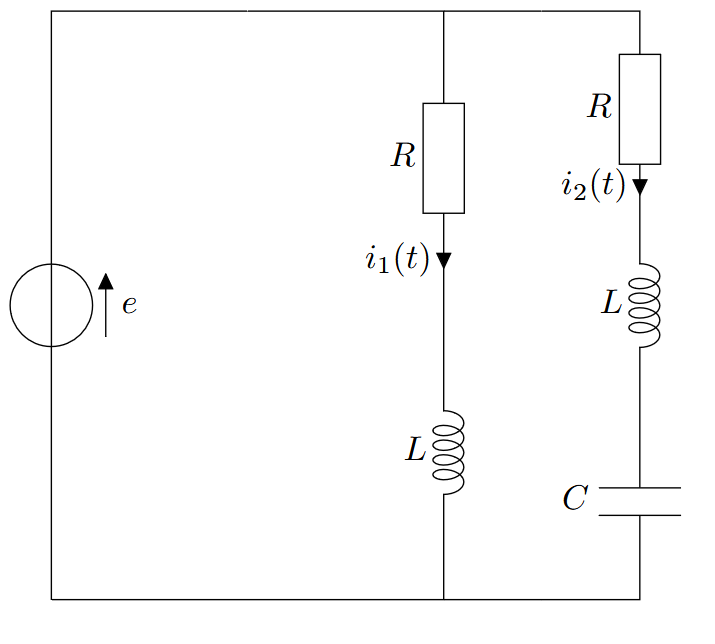
Exercice 4 : Intensité 2

Le circuit est alimenté par un générateur de tension sinusoïdale $e = E_0 cos(\omega t)$, avec $\omega$ telle que : $R = L \times \omega = \frac{1}{C \omega}$. Déterminer l’intensité circulant dans la résistance de droite.

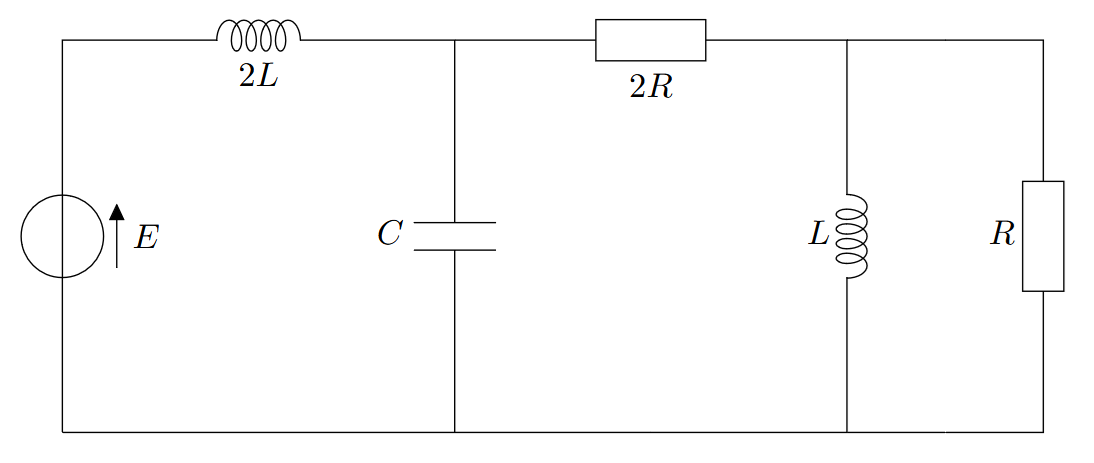
Exercice 5 : Phase

Le circuit suivant est alimenté par un générateur de tension sinusoïdale $e = E_0 \sin(\omega t)$.

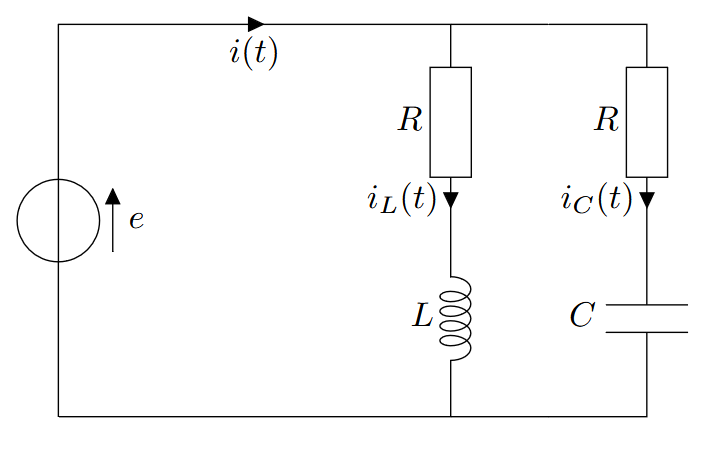
1. Exprimer l’impédance totale du circuit.

2. Exprimer les intensités $i, i_L, i_C$.

3. Donner une relation entre $R, L, C$ pour que l’intensité $i$ soit en phase avec la tension $e$.