Chapitre 0 : Outils mathématiques

Coordonnées cartésiennes, polaires, et sphériques

Il est d’usage en physique d’utiliser un système de coordonnées approprié au problème que l’on va traiter.

Coordonnées cartésiennes

De manière générale, on utilise le système des coordonnées cartésiennes, où un point est repéré par ses côtes le long des axes $Ox,Oy,Oz$

Coordonnées polaires

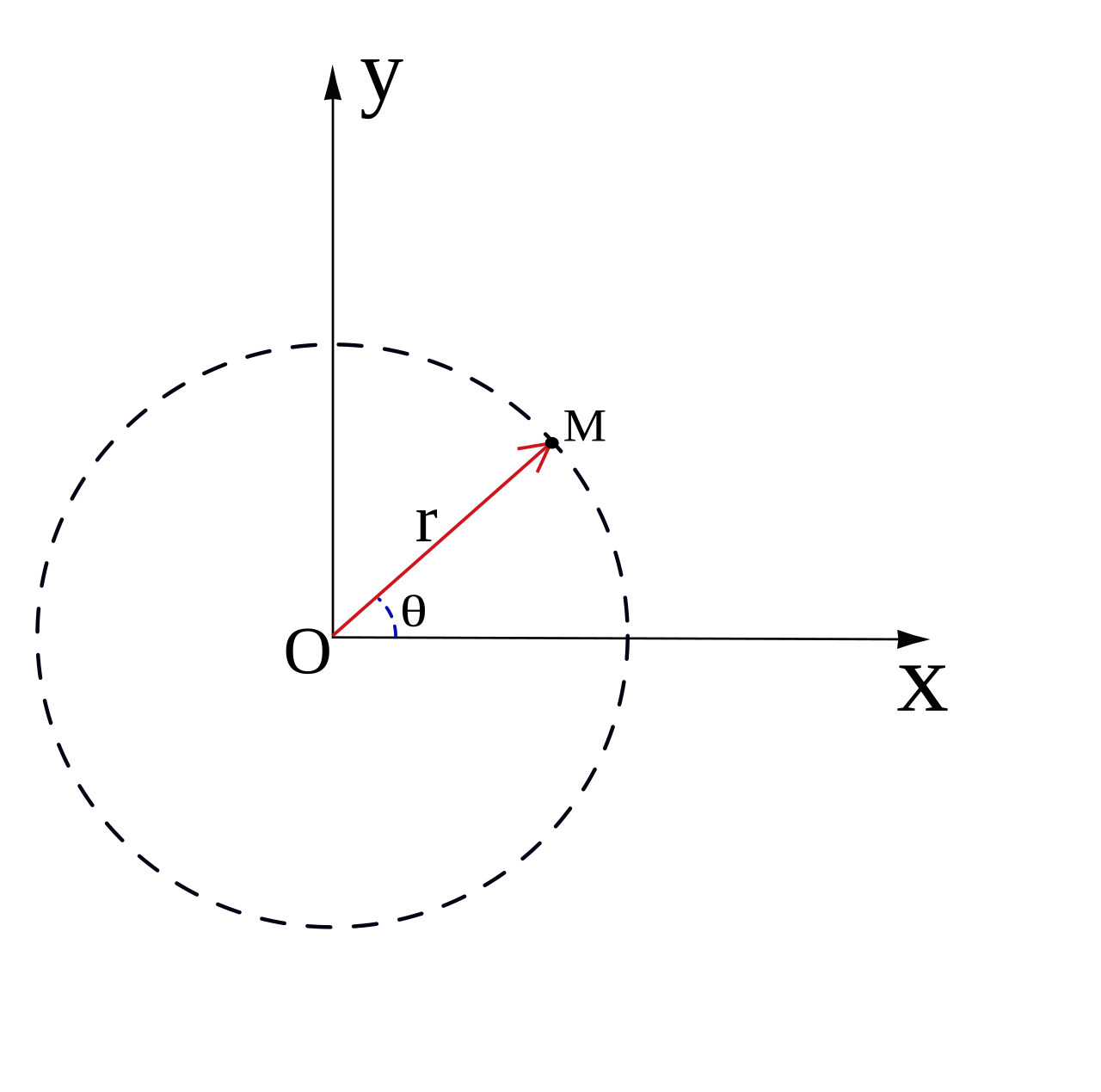
Dans un plan, on peut également considérer les coordonnées polaires : au lieu de considérer l’abcisse $x$ et l’ordonnée $y$ d’un point, on va plutôt le repérer via sa distance à l’origine $r$ et l’angle formé avec l’axe des abcisses $\theta$.

On a : $r = \sqrt{x^2+y^2}$ et $\theta = \arctan (\frac{y}{x}) \pm \pi$

Et à l’inverse : $x = r \cos (\theta)$ et $y = r \sin (\theta)$

Coordonnées cylindriques

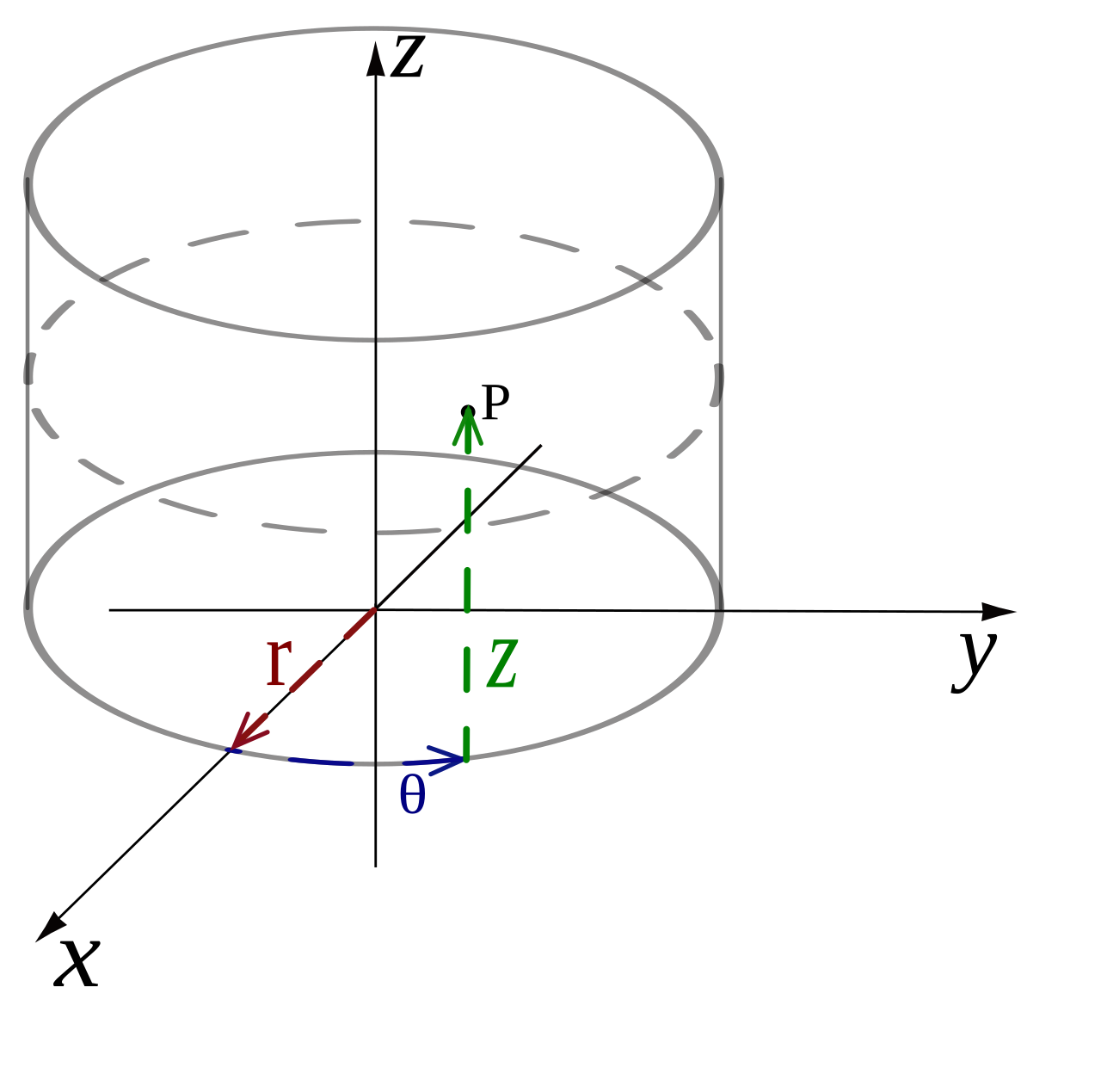
On peut généraliser le concept des coordonnées cylindriques dans un espace à 3 dimensions, en ajoutant la hauteur $z$ du point considéré. Les calculs restent les mêmes.

Coordonnées sphériques

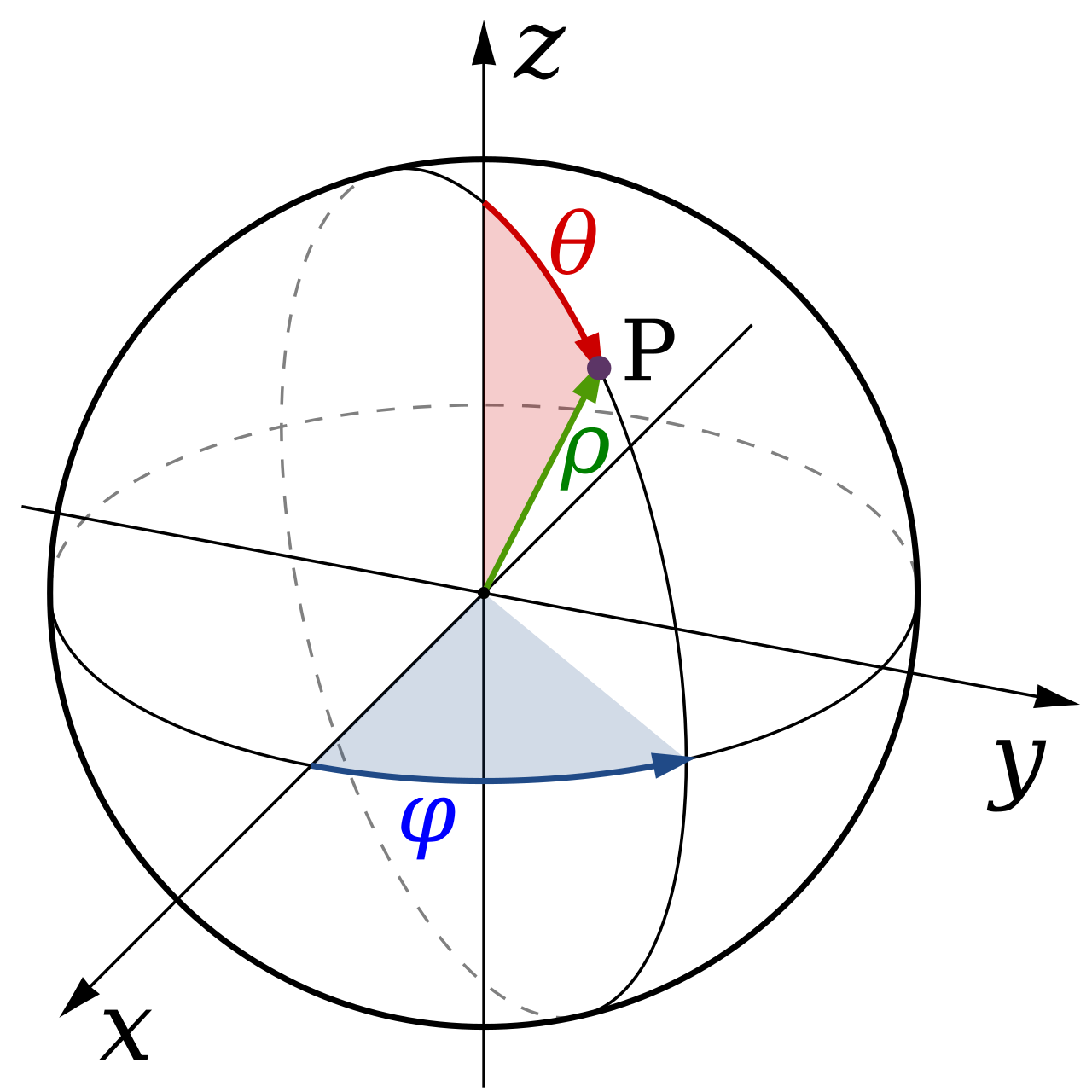
Il s’agit maintenant de repérer un point dans un espace à 3 dimensions, armé de deux angles et une distance (penser latitude/longitude).

On a maintenant : $\rho = \sqrt{x^2+y^2+z^2}$, $\varphi = \arctan(\frac{y}{x})$, et $\theta = \arccos(\frac{z}{\rho})$

Et à l’inverse : $x = \rho \sin(\theta)\cos(\varphi)$, $y = \rho \sin(\theta)\sin(\varphi)$, et $z = \rho \cos(\theta)$

Chapitre 1 : Champ électrique et magnétique

Qu’est-ce que la charge électrique ?

Quand on parle de gravité / d’interaction gravitationnelle, on sait que tout corps massique est à la fois une source de champ gravitationnel (i.e. il peut attirer tout autre corps massique) mais peut également interagir avec tout champ gravitationnel (i.e. il peut être attiré par tout autre corps massique).

Les particules chargées électriquement agissent de la même manière, à la différence près qu’elles peuvent être chargées négativement.

On appelle charge élémentaire la valeur $e = 1.6\times 10^{-19} C$, qui correspond à la valeur absolue de la charge d’un électron.

Champ électrique : sources et interactions

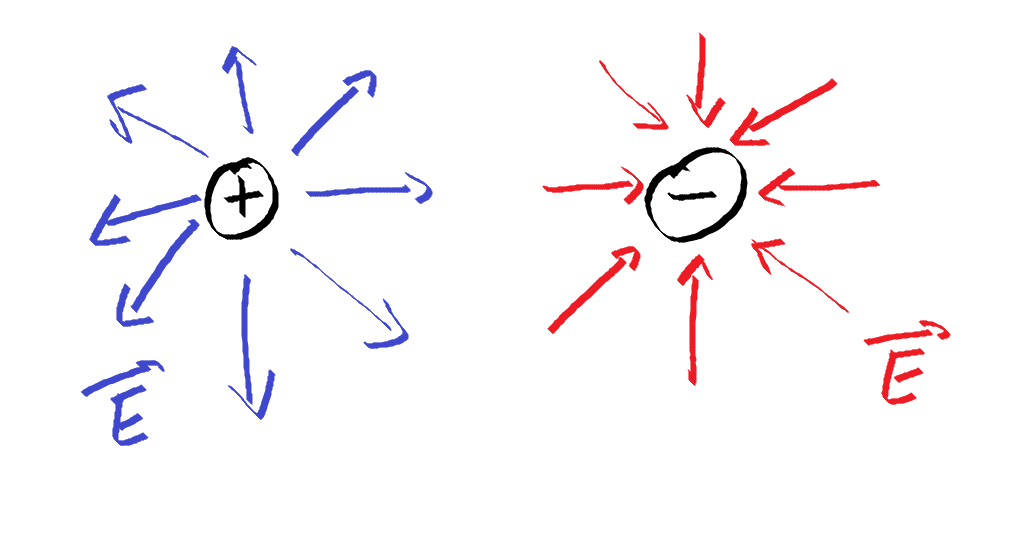
Le champ électrique est créé par les charges électriques. Il diverge à partir des charges positives et converge vers les charges négatives. Il n’a pas de caractère tourbillonant autour de celles-ci.

Le champ électrostatique créé par une particule de charge $q$ et à la distance $r$ de celle-ci s’exprime :

\[\vec{E} = \dfrac{q}{4\pi\varepsilon_0 r^2}\vec{u}\]

$\varepsilon_0$ est une constante nommée permittivité du vide, $\varepsilon_0 = 8.85\times 10^{-12}F.m^{-1}$

Remarque : il sera de bon ton de se demander comment le vecteur $\vec{u}$ est orienté en se référant à la remarque précédente.

Remarque : le champ électrique prend donc une valeur différente en tout point de l’espace. On peut observer que la dépendance en $1/r^2$ signifie que plus on s’éloigne d’une particule, moins l’intensité du champ généré par celle-ci est élevé.

De plus, l’interaction de toute charge avec un champ électrique s’exprime par le biais de la force :

\[\vec{F}_e = q\vec{E}\]

Lorsque l’intensité de ce champ électrique est constante dans le temps, on parlera de champ électrostatique.

Champ magnétique : sources

Le champ magnétique, quant à lui, est créé par les mouvements de charges électriques (en d’autres termes : du ‘courant électrique’). Il est donc plus difficile d’obtenir des équations simples permettant de le caractériser, puisqu’il faut caractériser le mouvement des charges !

Afin de simplifier l’étude ici, nous allons considérer quelques cas particuliers (et qui se retrouvent assez souvent dans notre quotidien) de génération de champ magnétique par des géométries particulières.

À la différence du champ électrique, nous allons voir que le champ magnétique présente un caractère tourbillonnant autour des mouvements de charges électriques (on parle d’un champ rotationnel)

Remarque : quelques visualisations intéressantes peuvent être trouvées ici : https://www.youtube.com/watch?v=rB83DpBJQsE

Théorème d’Ampère

Le théorème d’Ampère va nous permettre de calculer le champ magnétique le long d’un contour fermé (cf ci-après) :

\[\oint \vec{B}\vec{d\ell} = \mu_0 I_{enl}\]

Quelques explications sur les différents termes :

• $\oint$ représente une intégrale sur un contour fermé (par exemple, un cercle est un contour fermé, un segment ne l’est pas)
• En fonction de l’orientation de ce contour (donc du sens dans lequel on intègre), la surface attenante sera elle aussi orientée dans une direction.
• $\vec{B}$ est le champ magnétique
• $\mu_0$ est une constante, nommée perméabilité du vide, $\mu_0 = 4\pi\times 10^{-7}H.m^{-1}$
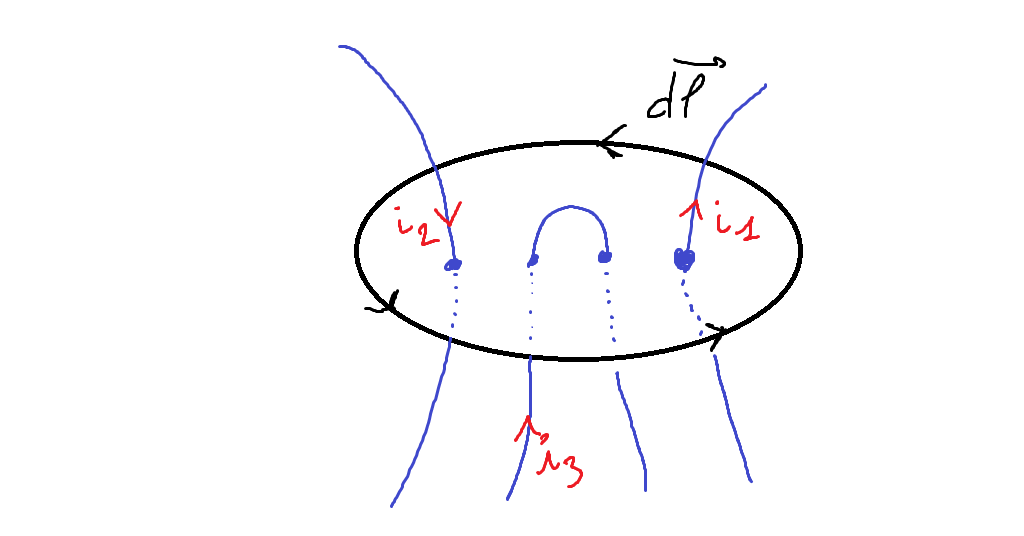
• $I_enl$ correspond à l’intensité électrique ‘enlacée par le contour’ (cf figure ci-dessous).

L’orientation de la surface peut se faire à l’aide de la règle du tire-bouchon : en tournant le tire-bouchon dans le sens de parcours du contour, le sens de déplacement du manche du tire-bouchon indique l’orientation de $\vec{S}$

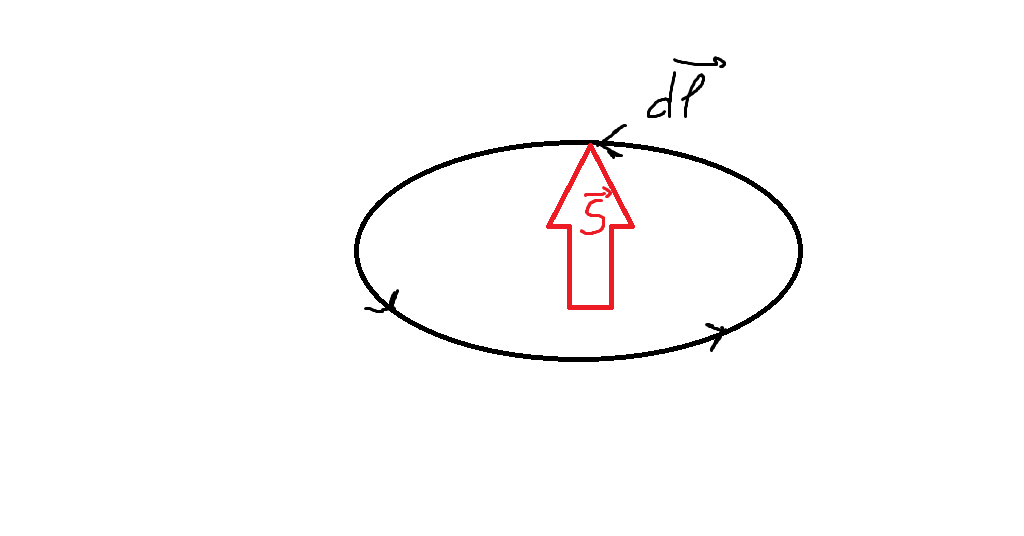
L’intensité électrique enlacée se calcule ensuite en additionnant algébriquement les intensités traversant la surface orientée : dans la figure suivante, $I_{enl} = i_1 -i_3 +i_3 -i_2$

Champ magnétique généré par un fil rectiligne

Quel est le champ magnétique créé par un fil infini, infiniment fin, parcouru par une intensité $I$ ?

Champ magnétique dans un solénoïde

Quel est le champ magnétique créé par un solénoïde de longueur infini, composé de $N$ spires jointives, et parcouru par une intensité électrique $I$ ?

Champ magnétique généré par une spire

Quel est le champ magnétique créé sur l’axe d’une spire, parcouru par une intensité $I$ ?

Qu’en est-il pour une superposition de $n$ spires ?

Champ magnétique : interactions

L’interaction d’une particule chargée avec un champ magnétique s’exprime selon la force suivante :

\[\vec{F_m} = q\vec{v}\wedge\vec{B}\]

où $q$ représente la charge de la particule, $\vec{v}$ sa vitesse.

Remarque : Une particule n’est soumise à l’action du champ magnétique que si elle est en mouvement ($\vec{v}=\vec{0} \implies \vec{F_m}=\vec{0}$)

Il est assez classique en physique de regrouper les forces dûes aux champ électriques et magnétique sous une seule et même force, appellée force de Lorentz :

\[\vec{F_L} = q(\vec{E} + \vec{v}\wedge\vec{B})\]

Exercices :

Exercice 1 : Calcul de champs magnétiques

Fils rectilignes :

On considère deux fils électriques (infiniment fins), orientés tous les deux selon l’axe $(Ox)$, espacés d’une distance $d$ selon l’axe $(Oy)$, parcourus respectivement d’une intensité éléctrique $i_1$ et $i_2$

1. Schématiser la situation
2. Donner le champ magnétique généré par l’ensemble en tout point de l’axe $(Oy)$

Solénoïdes concentriques :

On considère deux solénoïdes d’axe commun $(Oz)$, le premier de rayon $R_1$ parcouru par une intensité $i_1$, le second de rayon $R_2 > R_1$ parcouru par une intensité $i_2$. Les deux solénoïdes sont de longueur $L » R$ et ont un nombre de spires total $N$.

1. Schématiser la situation
2. Donner le champ magnétique généré par l’ensemble en tout point de l’axe $(Oz)$

Câble coaxial :

Quel est le champ magnétique généré par un câble coaxial ?

Exercice 2 : Accélération et déflection

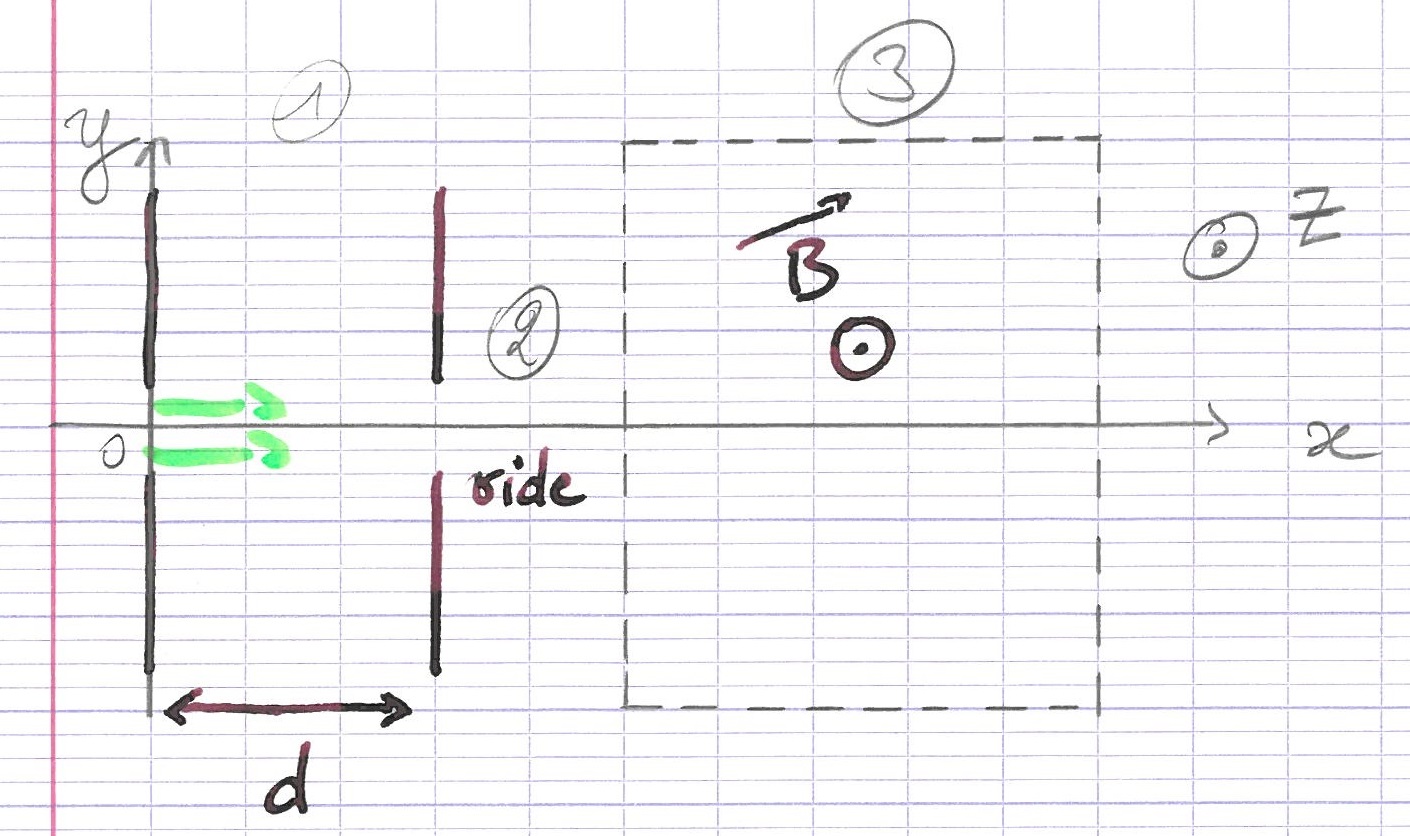
On considère le système représenté sur le schéma précédent.

Un faisceau de particules (chargées) traverse successivement :

• Une paire de plaques parallèles, situées en $x=0$ et $x=d$, sont alimentées par des tensions $\pm \frac{U}{2}$. Ceci créé un champ électrostatique (considéré uniforme et stationnaire) d’amplitude $E = \frac{U}{d}$. Les plaques sont percées de trous permettant à un faisceau de particules de traverser l’ensemble.
• Une zone considérée comme vide
• Une zone dans laquelle règne un champ magnétique uniforme et stationnaire, $\vec{B} = B_0 \vec{u_z}$ On considère que les particules entrent dans le système avec une vitesse nulle.

Données :

• charge d’un électron : $e = -1.6\times 10^{-19}C$
• masse d’un électron : $m_e = 9.1\times 10^{-31}kg$
• tension : $U = 3 000 V$
• distance entre les plaques : $d = 5cm$

1. Dans quel sens doit être le champ électrique de la première zone afin d’accélérer des électrons ?
2. En déduire quelle plaque présente une tension positive / négative.
3. En considérant que l’on néglige le poids, effectuer un bilan des forces dans la zone 1.
4. À quelle vitesse sort un électron de la zone 1 ?
5. En considérant que l’on néglige le poids, effectuer un bilan des forces dans la zone 3.
6. Comment évolue la vitesse de l’électron ? (amplitude et direction)
7. Quel est l’intérêt d’un tel dispositif ? (Hint : si le faisceau de départ contient des particules de même charge mais de masse différente, que se passe-t-il ?)