Induction

Pré-requis : Bases d’électronique analogique.

L’induction électromagnétique est un phénomène physique découvert au cours du XIXè siècle. Ce phénomène se traduit par l’apparition d’un courant électrique dans un circuit en interaction avec un champ magnétique (sous certaines conditions).

Question : dans quels dispositifs utilisés de manière quotidienne rencontre-t-on le phénomène d’induction ?

On étudiera deux cas dans le cadre de ce cours :

• un circuit en mouvement dans un champ magnétique uniforme et stationnaire : l’induction de Lorentz
• un circuit immobile dans un champ magnétique variable : l’induction de Neumann

Remarque : n’oubliez pas votre tire-bouchon !

Lois basiques de l’induction

Loi de Faraday

Remarque pour les élèves de prépa : il s’agit de la traduction intégrale de l’équation de Maxwell-Faraday

Les variation de flux magnétique au travers d’un circuit fermé se modélisent par l’ajout d’un générateur dans le circuit. On dit alors que la force électromotrice (f.e.m) induite $e$ est reliée au flux magnétique $\Phi$ par :

\[e = \dfrac{-d \Phi}{dt}\text{ avec }\Phi = \int\int_{circuit} \vec{B}\vec{dS}\]

Remarque : la surface $\vec{dS}$ est orientée par règle de la main droite par rapport au sens conventionnel du courant

Re-remarque : la force électromotrice induite $e$ est alors orientée en convention générateur par rapport à $i$ (dans le même sens)

Exemples :

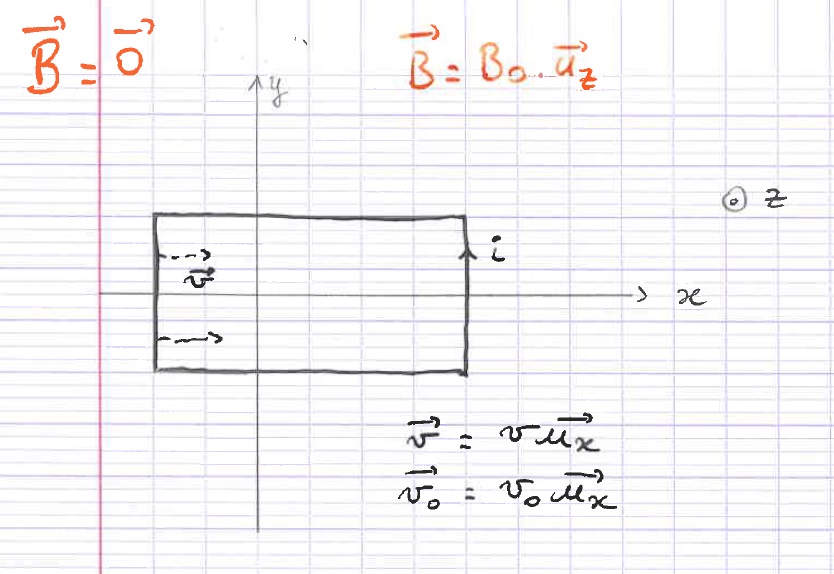
Dans le cas de l’induction de Lorentz, on a un circuit en mouvement dans un champ magnétique $\vec{B}$ uniforme. Dans ce cas, $\vec{B}$ est constant, mais $S$ ne l’est pas.

On a alors :

$e = \dfrac{-d \Phi}{dt}$

$= - B_0 \dfrac{dS}{dt}$

$= -B_0 \ell \dfrac{dx}{dt}$

où $\ell$ est la largeur du circuit considéré.

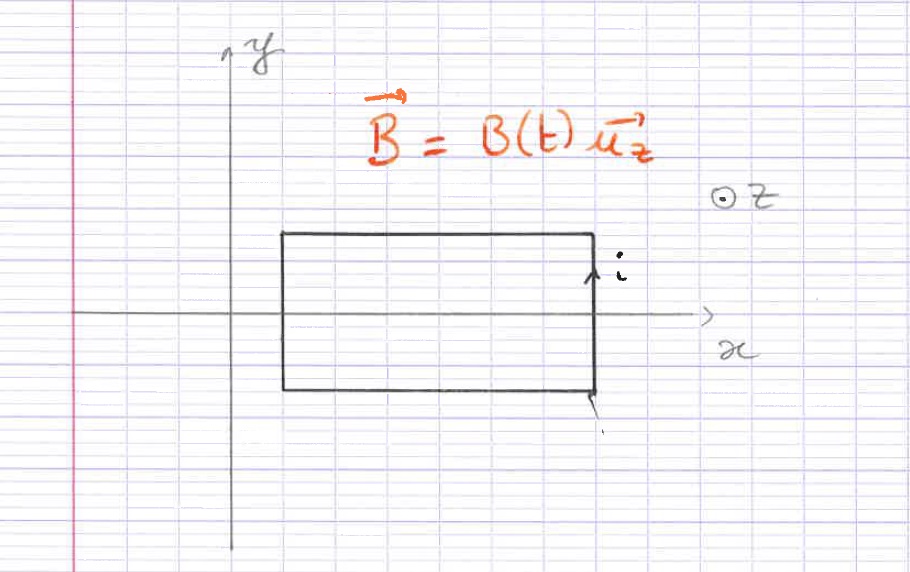
Dans le cas de l’induction de Neumann, le circuit est fixe, mais le champ est variable. Dans ce cas, $S$ est constant, mais $\vec{B}$ ne l’est pas.

On a alors :

$e = \dfrac{-d \Phi}{dt}$

$= - S \dfrac{dB(t)}{dt}$

Loi de Lenz

Induction $\rightarrow$ modération

En d’autres termes, les phénomènes d’induction tendent à atténuer leur cause.

C’est ce qu’on appelle une loi de modération

Pour le phénomène d’induction, la cause est toujours la même : il s’agit d’une variation du flux magnétique $\Phi$.

• Si cette variation de flux est dûe à une variation du champ magnétique $\vec{B}$, alors le champ magnétique induit aura tendance à atténuer ces variations de flux.
• Si cette variation de flux est dûe à un mouvement du circuit, alors la force de Laplace induite va avoir tendance à s’opposer au mouvement initial.

Force de Laplace

Rappel : \(\vec{F_m} = q\vec{v}\wedge \vec{B}\)

Comme mentionné dans le chapitre précédent, toute charge en mouvement est soumise à une interaction avec le champ magnétique.

Dans le cas de l’induction de Lorentz :

• Le mouvement d’un circuit au sein d’un champ magnétique (stationnaire et uniforme) induit un courant électrique au sein de ce circuit.
• Ce courant électrique va donc engendrer un mouvement de charge
• Ce mouvement de charge va entraîner une interaction avec le champ magnétique, et donc une action mécanique sur le circuit

On appelle force de Laplace l’action mécanique exercée par un champ magnétique sur un circuit électrique parcouru par un courant.

\[d\vec{F}_{Lap} = i\vec{d\ell}\wedge\vec{B}\]

On orientera le vecteur $\vec{d\ell}$ dans le même sens que $i$ pour que l’expression soit valable. Pour obtenir l’expression de la force de Laplace totale, il faudra ensuite intégrer cette expression sur la totalité du circuit.

Sur un fragment de circuit rectiligne, on pourrait écrire : $\vec{F_L} = i \vec{L}\wedge\vec{B}$ où $\vec{L}$ représente le vecteur orienté dans le sens de l’intensité, et de longueur correspondant à la longueur du segment considéré.

Remarque : dans le cas d’un circuit fermé plongé entièrement dans un champ magnétique uniforme, $\vec{F_L} = \vec{0}$

Exercice-type : freinage magnétique

On reprend le schéma :

On imagine que le circuit en mouvement est accroché à un véhicule, en mouvement selon la direction $x$, à une vitesse $\vec{v_0} = v_0 \vec{u_x}$. Dans l’espace $x<0$, le champ magnétique est nul, et dans l’espace $x>0$, $\vec{B} = B_0 \vec{u_z}$.

On considère que le circuit présente une résistance totale $R_{int}$.

On note $x_C$ l’abcisse de la branche droite du circuit. Pour $x_C<0$, il n’y a aucune interaction car $\vec{B} = \vec{0}$. Notre étude va se concentrer sur la zone : $0<x_C<L$, $L$ étant la longueur dans la direction $x$ du circuit, et $\ell$ la largeur dans la direction $y$ du circuit.

1. Équation électrique :

On peut calculer la force électromotrice induite via la loi de Faraday :

$e = \dfrac{-d\Phi}{dt}$

$= -B_0\dfrac{dS}{dt}$

$= -B_0 \ell \dfrac{dx}{dt}$

Ceci a donc pour effet de créer un courant électrique induit :

$i_I = \dfrac{e}{R_{int}}$

$= -\dfrac{B_0 \ell}{R_{int}} \dfrac{dx}{dt}$

1. Équation mécanique :

On considère que le circuit n’est soumis qu’à la force de Laplace résultante (déplacement sans frottement, poids compensé par la réaction du support … imaginez un train magnétique japonais)

On rappelle l’expression de la force de Laplace : $\vec{F_L} = i \vec{L}\wedge\vec{B}$.

À un instant donné, le segment vertical a pour ‘vecteur longueur’ $\ell \vec{u_y}$. Les segments horizontaux ont quant à eux pour ‘vecteur longueur’ $\pm x_c \vec{u_x}$.

La force de Laplace totale est donc :

$\vec{F_L} = i_I x_c \vec{u_x} \wedge \vec{B} + i_I \ell \vec{u_y} \wedge \vec{B} + i_I (-x_c) \vec{u_x} \wedge \vec{B}$

Les termes 1 et 3 s’annulent !

$\vec{F_L} = i_I \ell \vec{u_y} \wedge \vec{B}$

$= (i_I \ell \vec{u_y}) \wedge (B_0 \vec{u_z})$

$= i_I \ell B_0 \vec{u_y}\wedge\vec{u_z}$ $= i_I \ell B_0 \vec{u_x}$ $= -\dfrac{B_0 \ell}{R_{int}} \dfrac{dx}{dt}\ell B_0 \vec{u_x}$ \(\vec{F_L}= -\dfrac{B_0^2 \ell^2}{R_{int}} \dfrac{dx}{dt}\vec{u_x}\)

On obtient donc une force opposée au mouvement (la loi de Lenz est vérifiée).

1. Épilogue

On peut appliquer le PFD au système total :

\[m\dfrac{d^2 x}{dt^2} = -\dfrac{B_0^2 \ell^2}{R_{int}} \dfrac{dx}{dt}\]

(les vecteurs peuvent être simplifiés, le mouvement est purement selon l’axe $(Ox)$)

Cette équation peut être ré-écrite en une équation différentielle linéaire d’ordre 1 sur la vitesse en $x$ :

\[m\dfrac{d v_x}{dt} + \dfrac{B_0^2 \ell^2}{R_{int}} v_x = 0\] \[\iff \dfrac{d v_x}{dt} + \dfrac{B_0^2 \ell^2}{m R_{int}} v_x = 0\]

On en déduit finalement : $v_x(t) = v_0 \exp(-\frac{B_0^2 \ell^2}{m R_{int}}t)$

Moment magnétique d’un circuit

Couple

Exercices

Exercice 1 : Rails de Laplace, moteur

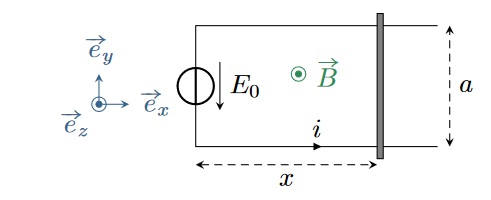
Considérons un système de rails de Laplace séparés d’une distance $a$ et soumis à un champ magnétique extérieur $\vec{B} = B\vec{e_z}$. L’ensemble possède une résistance électrique $r$. Ce système est utilisé en fonctionnement moteur : un générateur impose une tension $E_0$, ce qui met en mouvement la tige initialement immobile. Il réalise donc une conversion d’énergie électrique en énergie mécanique.

1. Exprimer la force de Laplace subie par la tige mobile. En déduire l’équation mécanique.
2. Déterminer la force électromotrice induite. En déduire l’équation électrique.
3. Établir et résoudre l’équation différentielle vérifiée par la vitesse $v_x$ de la tige.
4. Établir et résoudre l’équation différentielle vérifiée par l’intensité $i$.
5. Comparer la puissance mécanique fournie par la force de Laplace et la puissance électrique fournie par le générateur induit. Interpréter physiquement leur signe respectif.
6. Procéder au bilan de puissance, et l’interpréter.

Exercice 2 : Rails de Laplace, générateur

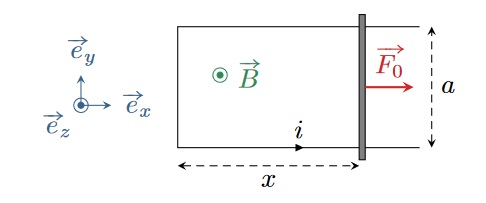
Considérons les mêmes rails de Laplace que dans l’exercice précédent. Le système est maintenant utilisé en fonctionnement générateur : il n’y a plus de fénérateur $E_0$, mais un opérateur extérieur tracte la tige (intialement immobile) avec une force constante $\vec{F_0}$, ce qui génère un courant induit dans le système. Il réalise donc une conversion d’énergie mécanique en énergie électrique.

1. Déterminer sans calcul le signe du courant induit.
2. Exprimer la force de Laplace subie par la tige mobile. En déduire l’équation mécanique.
3. Déterminer la force électromotrice induite. En déduire l’équation électrique.
4. Établir et résoudre l’équation différentielle vérifiée par l’intensité $i$.
5. Comparer la puissqnce mécanique fournie par la force de Laplace et la puissance électrique fournie par le générateur induit.
6. Procéder au bilan de puissance et l’interpréter.